【题目】已知a,b,c,d都不等于0,并且![]() , 根据分式的基本性质、等式的基本性质及运算法则,探究下面各组中的两个分式之间有什么关系?然后选择其中一组进行具体说明.
, 根据分式的基本性质、等式的基本性质及运算法则,探究下面各组中的两个分式之间有什么关系?然后选择其中一组进行具体说明.
(1)![]() 和
和![]() ; (2)
; (2)![]() 和
和![]() ; (3)
; (3)![]() 和
和![]() (a≠b,c≠d).
(a≠b,c≠d).
参考答案:
【答案】解:例如:取a=1,b=2,c=3,d=6,有![]() ,
,
则(1)![]() ;
;
(2)![]() ;
;
(3)![]()
观察发现各组中的两个分式相等.
现选择第(2)组进行说明证明.
已知a,b,c,d都不等于0,并且![]() ,
,
所以有:![]() ,
,
所以有:![]() =
=![]() .
.
【解析】先利用具体的数计算,然后发现各组中的两个分式相等;再对(2)进行证明:等式两边加上1,通分即可.
【考点精析】本题主要考查了分式的基本性质的相关知识点,需要掌握分式的分子与分母同乘以或除以同一个不等于0的整式,分式的值不变才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天凌晨的气温是-5℃,中午的气温比凌晨上升4℃,那么中午的气温是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探索:
(1)已知一个正分数 (m>n>0),如果分子、分母同时增加1,分数的值是增大还是减小?请证明你的结论.
(m>n>0),如果分子、分母同时增加1,分数的值是增大还是减小?请证明你的结论.
(2)若正分数 (m>n>0)中分子和分母同时增加2,3…k(整数k>0),情况如何?
(m>n>0)中分子和分母同时增加2,3…k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问同时增加相等的窗户面积和地板面积,住宅的采光条件是变好还是变坏?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】购买单价为a元的物品10个,付出b元(b>10a),应找回( )
A. (b﹣a)元 B. (b﹣10)元 C. (10a﹣b)元 D. (b﹣10a)元
-
科目: 来源: 题型:
查看答案和解析>>【题目】求﹣(5a+b﹣ab)﹣(2ab﹣2a﹣4b)+(2b﹣2a﹣3ab) 的值.(其中a﹣b=5,ab=﹣3.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:
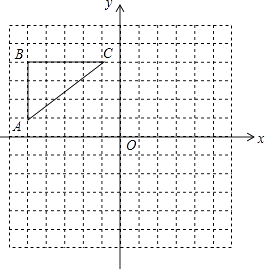
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是;点C2的坐标是;△ABC的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
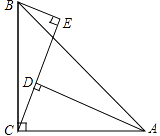
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
相关试题

