【题目】如图,一次函数![]() =
=![]() 的图像与正比例函数
的图像与正比例函数![]() =
=![]() 的图像相交于点A(2,
的图像相交于点A(2,![]() ),与
),与![]() 轴相交于点B.
轴相交于点B.

(1)求![]() 、
、![]() 的值;
的值;
(2)在![]() 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
参考答案:
【答案】(1)a=1,b=2;(2)点C的坐标为(0,2)或(0,-2).
【解析】
(1)利用正比例函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标,利用待定系数法即可求出b的值;
(2)利用一次函数图象上点的坐标特征可求出点B的坐标,根据三角形的面积公式结合△AOC的面积等于△AOB的面积,即可得出点C的坐标.
解:(1)把点A(2,a)的坐标代入y=![]() x,解得a=1.
x,解得a=1.
把点A(2,1)的坐标代入y=-![]() x+b,解得b=2.
x+b,解得b=2.
(2)把y=0代入y=-![]() x+2,解得x=4.
x+2,解得x=4.
∴点B的坐标为(4,0).
∴OB=4.
∵S△AOC=S△AOB,
∴![]() ×2·OC=
×2·OC=![]() ×4×1.
×4×1.
∴OC=2.
∴点C的坐标为(0,2)或(0,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.

(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91) -
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法,例如:
①用配方法分解因式:
 .
.解:原式

②
 ,利用配方法求
,利用配方法求 的最小值.
的最小值.解:
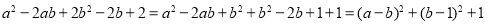
∵
 ,
,
∴当
 时,
时, 有最小值1.
有最小值1.请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:
 ________.
________.(2)用配方法因式分解:
 .
.(3)若
 ,求
,求 的最小值.
的最小值.(4)已知
 ,则
,则 的值为________.
的值为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
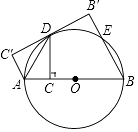
(1)请你判断C′D与⊙O的位置关系,并说明理由;
(2)过点B作BB′⊥C′D′于B′,交⊙O于E,若CD= ,AC=3,求BE的长.
,AC=3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当
 时,求
时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极支持鄂州市创建国家卫生城市工作,某商家计划从厂家采购A,B两种清洁产品共20件,产品的采购单价(元/件)是采购数量(件)的相关信息如下表所示.
采购数量(件)
2
4
6
…
A产品单价(元)
1460
1420
1380
…
B产品单价(元)
1280
1260
1240
…
(1)设B产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在
 中,
中, ,
, 平分
平分 ,
, 为直线
为直线 上一点,
上一点, ,
, 为垂足,
为垂足, 的平分线交直线
的平分线交直线 于点
于点 ,回答下列问题并说明.(可在图上标注数字角)
,回答下列问题并说明.(可在图上标注数字角)(1)如图①,
 为边
为边 上一点,则
上一点,则 、
、 的位置关系是________.请给予证明;
的位置关系是________.请给予证明;
(2)如图②,
 为边
为边 反向延长线上一点,则
反向延长线上一点,则 、
、 的位置关系是________.(请直接写出结论)
的位置关系是________.(请直接写出结论)
(3)如图③,
 为边
为边 延长线上一点,则
延长线上一点,则 、
、 的位置关系是________.请给予证明.
的位置关系是________.请给予证明.
相关试题

