【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() 为直线
为直线![]() 上一点,
上一点,![]() ,
,![]() 为垂足,
为垂足,![]() 的平分线交直线
的平分线交直线![]() 于点
于点![]() ,回答下列问题并说明.(可在图上标注数字角)
,回答下列问题并说明.(可在图上标注数字角)
(1)如图①,![]() 为边
为边![]() 上一点,则
上一点,则![]() 、
、![]() 的位置关系是________.请给予证明;
的位置关系是________.请给予证明;

(2)如图②,![]() 为边
为边![]() 反向延长线上一点,则
反向延长线上一点,则![]() 、
、![]() 的位置关系是________.(请直接写出结论)
的位置关系是________.(请直接写出结论)

(3)如图③,![]() 为边
为边![]() 延长线上一点,则
延长线上一点,则![]() 、
、![]() 的位置关系是________.请给予证明.
的位置关系是________.请给予证明.

参考答案:
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ;(3)
;(3)![]() ,见解析
,见解析
【解析】
(1)根据∠A=90°,![]() ,得∠CME=∠ABC,再由四边形内角和知∠ABC+∠AME=180°,再由BD平分∠ABC,ME平分∠AME可得
,得∠CME=∠ABC,再由四边形内角和知∠ABC+∠AME=180°,再由BD平分∠ABC,ME平分∠AME可得![]() ,
,![]() ,即得到
,即得到![]() ,
,
(2)由题意可以得到∠AME=∠ABC,又由BD平分∠ABC,ME平分∠AME可以得到∠AMF=∠ABD,即可得到∠AMF+∠ADB=90°即可得到![]() ,
,
(3)先根据题意延长BD交EF于N,根据题意得出∠ABD=∠DMN,再根据三角形内角和即可得出![]() .
.
解:(1)![]()
证明:∵![]() ,
,
∴![]() ;
;
∵在四边形![]() 中,
中,![]() ,
,
∴![]() ;
;
∵![]() 平分
平分![]() ,
,
∴![]() ;
;
同理![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]()
(3)![]()
证明:延长![]() 交
交![]() 于点
于点![]() ,
,
在![]() 与
与![]() 中
中
![]()
∵![]() 与
与![]() 为对顶角,
为对顶角,
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
∵![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
在![]() 与
与![]() 中
中
![]() ,
,
∵![]() 与
与![]() 为对顶角,
为对顶角,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 =
= 的图像与正比例函数
的图像与正比例函数 =
= 的图像相交于点A(2,
的图像相交于点A(2, ),与
),与 轴相交于点B.
轴相交于点B.
(1)求
 、
、 的值;
的值;(2)在
 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当
 时,求
时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为积极支持鄂州市创建国家卫生城市工作,某商家计划从厂家采购A,B两种清洁产品共20件,产品的采购单价(元/件)是采购数量(件)的相关信息如下表所示.
采购数量(件)
2
4
6
…
A产品单价(元)
1460
1420
1380
…
B产品单价(元)
1280
1260
1240
…
(1)设B产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
,且B产品采购单价不高于1250元,求该商家共有几种进货方案?
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大?并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好
 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.10月1日
2日
3日
4日
5日
6日
7日
4
3
2
0



 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天? 直接回答,不必写过程
直接回答,不必写过程 .
. 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.已知,
 中,
中, ,
, ,点
,点 、
、 在边
在边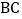 上,且
上,且 .
.
(1)如图
 ,当
,当 时,将
时,将 绕点
绕点 顺时针旋转
顺时针旋转 到
到 的位置,连接
的位置,连接 ,
,①求
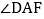 的度数;
的度数;②求证:
 ;
;(2)如图
 ,当
,当 时,猜想
时,猜想 、
、 、
、 的数量关系,并说明理由;
的数量关系,并说明理由;(3)如图
 ,当
,当 ,
, ,
, 时,请直接写出
时,请直接写出 的长为________.
的长为________.
相关试题

