【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法,例如:
①用配方法分解因式:![]() .
.
解:原式![]()
②![]() ,利用配方法求
,利用配方法求![]() 的最小值.
的最小值.
解:![]()
∵![]() ,
,![]()
∴当![]() 时,
时,![]() 有最小值1.
有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]() ________.
________.
(2)用配方法因式分解:![]() .
.
(3)若![]() ,求
,求![]() 的最小值.
的最小值.
(4)已知![]() ,则
,则![]() 的值为________.
的值为________.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4;(4)4
;(3)4;(4)4
【解析】
(1)根据题意,由完全平方公式![]() ,可以知道横线上是
,可以知道横线上是![]() ,
,
(2)按照题干上的示例可以将![]() 分为
分为![]() ,再利用完全平方公式即可求解,
,再利用完全平方公式即可求解,
(3)根据题意的方法,先将M因式分解为完全平方的形式即![]() ,即可求出最小值,
,即可求出最小值,
(4)根据题意先将![]() 因式分解,变成完全平方的形式即
因式分解,变成完全平方的形式即![]() ,然后得出x,y,z的值,代入
,然后得出x,y,z的值,代入![]() 即可求出结果.
即可求出结果.
解:(1)根据完全平方公式知:空上填![]() 即
即![]() ,故答案为
,故答案为![]() ,
,
(2)![]()
![]()
![]()
![]() ;
;
(3)![]()
![]()
![]()
![]() ;
;
∵![]() ,
,
∴![]() ,
,
∴![]() 的最小值是4;
的最小值是4;
(4)∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 、
、![]() 、
、![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
故答案为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称____ ___,___ ;(2分)
(2)如图,已知格点(小正方形的顶点)
 ,
, ,
, ,请你直接写出所有以格点为顶点,
,请你直接写出所有以格点为顶点, 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形 的顶点M的坐标。(3分)
的顶点M的坐标。(3分)
(3)如图,将
 绕顶点
绕顶点 按顺时针方向旋转
按顺时针方向旋转 ,得到
,得到 ,连结
,连结 ,
, .求证:
.求证: ,即四边形
,即四边形 是勾股四边形.(4分)
是勾股四边形.(4分)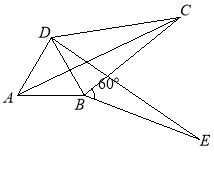
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象与x轴的两个交点为A(x1 , 0),B(x2 , 0),且x12+x22=25,求m的值;
(3)设该函数的图象的顶点为C,与x轴交于A,B两点,且△ABC的面积为1,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.

(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C为AB上一点,作CD⊥AB交⊙O于D,连接AD,将△ACD沿AD翻折至△AC′D.
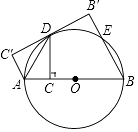
(1)请你判断C′D与⊙O的位置关系,并说明理由;
(2)过点B作BB′⊥C′D′于B′,交⊙O于E,若CD= ,AC=3,求BE的长.
,AC=3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 =
= 的图像与正比例函数
的图像与正比例函数 =
= 的图像相交于点A(2,
的图像相交于点A(2, ),与
),与 轴相交于点B.
轴相交于点B.
(1)求
 、
、 的值;
的值;(2)在
 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.
轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为
 (千克),在甲园所需总费用为
(千克),在甲园所需总费用为 (元),在乙园所需总费用为
(元),在乙园所需总费用为 (元),
(元), 、
、 与
与 之间的函数关系如图所示.
之间的函数关系如图所示.
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当
 时,求
时,求 与
与 的函数表达式;
的函数表达式;(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
相关试题

