【题目】已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A(m,y1),B(m+6,y2)两点都在该函数的图象上,当m=时,y1=y2 .
参考答案:
【答案】-1
【解析】解:∵x=1时,y=2;x=3时,y=2,
∴抛物线的解析式为直线x=2,
∵A(m,y1),B(m+6,y2)两点都在该函数的图象上,y1=y2 ,
∴2﹣m=m+6﹣2,
解得m=﹣1.
故答案为﹣1.
根据表中的对应值得到x=1和x=3时函数值相等,则得到抛物线的解析式为直线x=2,由于y1=y2 , 所以A(m,y1),B(m+6,y2)是抛物线上的对称点,则2﹣m=m+6﹣2,然后解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
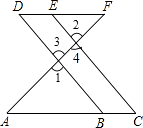
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2()
∠1=∠3()
∴∠2=∠3()
∴∥()
∴∠C=∠ABD ()
又∵∠C=∠D()
∴∠D=∠ABD()
∴AC∥DF() -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形一腰上的中线分周长为6cm或9cm两部分,求这个等腰三角形的底边和腰的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E.
(1)依题意补全图1;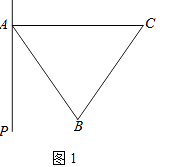
(2)若∠PAB=30°,求∠ACE的度数;
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明.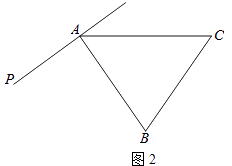
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2x-3y)M=9y2-4x2,则M表示的式子为______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
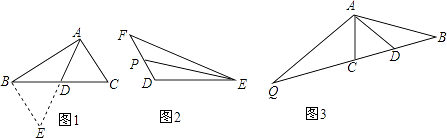
(1)【探究与发现】 如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形
(2)【理解与应用】 填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是
(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,计算结果正确的是( )
A.a2a3=a6
B.(a2)3=a5
C.(a2b)2=a2b2
D.(﹣a)6÷a=a5
相关试题

