【题目】下列命题中正确的有( )
①相等的角是对顶角.
②在同一平面内,若a∥b,b∥c,则a∥c.
③若点P(m+3,m+1)在x轴上,则点P的坐标为(4,0).
④数轴上每一个点都表示唯一一个实数.
⑤若a大于0,b不大于0,则点P(-a,-b)在第三象限.
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】B
【解析】分析: ①根据对顶角的定义进行判定, ②根据平行于同一条直线的两条直线平行进行判定, ③根据点在x轴上,纵坐标为0,可列方程求m,即可求出m点的坐标. ④根据数轴上的点与实数是一一对应的关系可判定, ⑤根据a大于0,确定-a是小于0,根据b不大于0,确定-b是大于等于0,再根据平面直角坐标系内点的坐标特征进行判定,坐标轴上的点不属于任何象限.
详解: ①因为对顶角是有一个公共顶点,且一个角的两边延长线是另一个角的两边,且对顶角相等,但相等的角不一定是对顶角,所以①表述错误,
②因为平行于同一条直线的两条直线平行,所以在同一平面内,若a∥b,b∥c,则a∥c,所以②表述正确,
③因为点P(m+3,m+1)在x轴上,所以m+1=0, m=-1,所以m+3=-2,则点P的坐标为(2,0),所以③表述不正确,
④因为数轴上的点与实数是一一对应的关系,所以数轴上每一个点都表示唯一一个实数,所以④表述正确,
⑤因为a大于0,b不大于0,所以![]() ,则点P(-a,-b)在第二象限或在x轴上,所以⑤表述错误,
,则点P(-a,-b)在第二象限或在x轴上,所以⑤表述错误,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2. 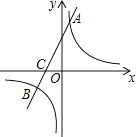
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点
 ,
, 满足
满足 .
. 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______. 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束 的中点D的坐标是
的中点D的坐标是 ,设运动时间为
,设运动时间为 秒
秒 问:是否存在这样的t,使
问:是否存在这样的t,使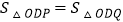 ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由. 点F是线段AC上一点,满足
点F是线段AC上一点,满足 ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中, 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2
 , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )
A. 2
 B. 4 C. 4
B. 4 C. 4 D. 8
D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】以下条件不能判别四边形ABCD是矩形的是( )
A. AB=CD,AD=BC,∠A=90° B. OA=OB=OC=OD
C. AB=CD,AB∥CD,AC=BD D. AB=CD,AB∥CD,OA=OC,OB=OD
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:cos60°﹣2﹣1+
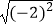 ﹣(π﹣3)0 .
﹣(π﹣3)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
相关试题

