【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2. 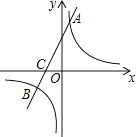
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
参考答案:
【答案】
(1)解:过点A作AD⊥x轴,垂足为D
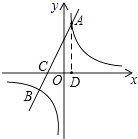
由A(n,6),C(﹣2,0)可得,
OD=n,AD=6,CO=2
∵tan∠ACO=2
∴ ![]() =2,即
=2,即 ![]() =2
=2
∴n=1
∴A(1,6)
将A(1,6)代入反比例函数,得m=1×6=6
∴反比例函数的解析式为 ![]()
将A(1,6),C(﹣2,0)代入一次函数y=kx+b,可得
![]()
解得 ![]()
∴一次函数的解析式为y=2x+4
(2)解:由 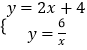 可得
可得 ![]()
![]()
解得x1=1,x2=﹣3
∵当x=﹣3时,y=﹣2
∴点B坐标为(﹣3,﹣2)
【解析】本题主要考查了反比例函数与一次函数的交点问题,解决问题的关键是掌握待定系数法求函数解析式.求反比例函数与一次函数的交点坐标时,把两个函数关系式联立成方程组求解,若方程组有解,则两者有交点,若方程组无解,则两者无交点.(1)先过点A作AD⊥x轴,根据tan∠ACO=2,求得点A的坐标,进而根据待定系数法计算两个函数解析式;(2)先联立两个函数解析式,再通过解方程求得交点B的坐标即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教师节要到了,为了表示对老师的敬意,小明做了两张大小不同的正方形壁画准备送给老师,其中一张面积为800 cm2,另一张面积为450 cm2,他想如果再用金彩带把壁画的边镶上会更漂亮,他现在有1.2 m长的金彩带,请你帮助算一算,他的金彩带够用吗?如果不够,还需买多长的金彩带?(
 ≈1.414,结果保留整数)
≈1.414,结果保留整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校住校生宿舍有大小两种寝室若干间,据统计该校高一年级男生740人,使用了55间大寝室和50间小寝室,正好住满;女生730人,使用了大寝室50间和小寝室55间,也正好住满.求该校的大小寝室每间各住多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.

(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点
 ,
, 满足
满足 .
. 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______. 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束 的中点D的坐标是
的中点D的坐标是 ,设运动时间为
,设运动时间为 秒
秒 问:是否存在这样的t,使
问:是否存在这样的t,使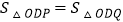 ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由. 点F是线段AC上一点,满足
点F是线段AC上一点,满足 ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中, 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2
 , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )
A. 2
 B. 4 C. 4
B. 4 C. 4 D. 8
D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的有( )
①相等的角是对顶角.
②在同一平面内,若a∥b,b∥c,则a∥c.
③若点P(m+3,m+1)在x轴上,则点P的坐标为(4,0).
④数轴上每一个点都表示唯一一个实数.
⑤若a大于0,b不大于0,则点P(-a,-b)在第三象限.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

