【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0) 
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
参考答案:
【答案】
(1)解:把点A(2,0)、B(﹣4,0)的坐标代入y=﹣x2+2bx+c得, ![]() ,
,
∴b=﹣1.c=8,
∴抛物线的解析式为y=﹣x2﹣2x+8
(2)解:如图1,
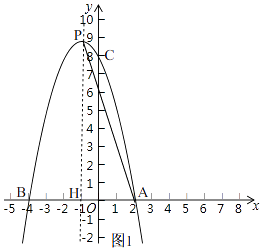
设抛物线的对称轴与x轴的交点为H,把点A(2,0)的坐标代入y=﹣x2+2bx+c得,
﹣4+4b+c=0①,
∵抛物线的顶点为P,
∴y=﹣x2+2bx+c=﹣(x﹣b)2+b2+c,
∴P(b,b2+c),
∴PH=b2+c,AH=2﹣b,
在Rt△PHA中,tan∠OAP= ![]() ,
,
∴ ![]() =3②,
=3②,
联立①②得, 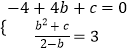 ,
,
∴ ![]() (不符合题意,舍)或
(不符合题意,舍)或 ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+8
(3)解:∵如图2,
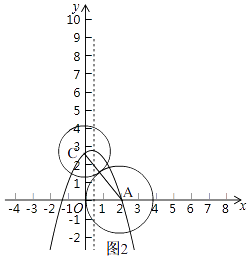
抛物线y=﹣x2+2bx+c与y轴正半轴交于点C,
∴C(0,c)(c>0),
∴ ![]() OC=
OC= ![]() c,
c,
∵A(2,0),
∴OA=2,
∴AC= ![]() ,
,
∵⊙A与⊙C外切,
∴AC= ![]() c+2=
c+2= ![]() ,
,
∴c=0(舍)或c= ![]() ,
,
把点A(2,0)的坐标代入y=﹣x2+2bx+c得,﹣4+4b+c=0,
∴b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+
x+ ![]() .
.
【解析】(1)利用待定系数法即可确定出函数解析式;(2)用tan∠OAP=3建立一个b,c的关系,再结合点A得出的等式即可求出b,c进而得出函数关系式;(3)用两圆外切,半径之和等于AC建立方程结合点A代入建立的方程即可得出抛物线解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD中,F是BC边的中点,连接DF并延长,交AB的延长线于点E.求证:AB=BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“626国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
少分数段(x表示分数)
频数
频率
50≤x<60
4
0.1
60≤x<70
a
0.2
70≤x<80
12
b
80≤x<90
10
0.25
90≤x<100
6
0.15

(1)表中a= , b= , 并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是;
(3)请估计该年级分数在60≤x<100的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察等式:①
 =1﹣
=1﹣  ;②
;② 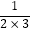 =
=  ﹣
﹣  ;③
;③ 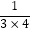 =
=  ﹣
﹣  ;④
;④ 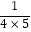 =
=  ﹣
﹣ 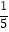 ,…
,…
(1)试用字母n的等式表示出你发现的规律,并证明该等式成立;
(2)
+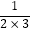 +
+ 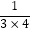 +…+
+…+ 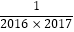 = . (直接写出结果)
= . (直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.

(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,线段A、B在格点上.

(1)将线段AB绕点O逆时针旋转90°得到线段A1B1 , 试在图中画出线段A1B1 .
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2 .
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形为平行四边形时,请你直接写出点P的坐标: .
相关试题

