【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
参考答案:
【答案】(1)45° (2)不发生改变,理由见解析
【解析】试题分析:(1)根据∠AOB是直角,∠AOC=40°,可得∠AOB+∠AOC=90°+40°=130°,再利用OM是∠BOC的平分线,ON是∠AOC的平分线,即可求得答案.
(2)根据∠MON=∠MOC﹣∠NOC,又利用∠AOB是直角,不改变,可得![]() .
.
解:(1)∵∠AOB是直角,∠AOC=40°,
∴∠AOB+∠AOC=90°+40°=130°,
∵OM是∠BOC的平分线,ON是∠AOC的平分线,
∴![]() ,
,![]() .
.
∴∠MON=∠MOC﹣∠NOC=65°﹣20°=45°,
(2)当锐角∠AOC的大小发生改变时,∠MON的大小不发生改变.
∵![]() =
=![]() ,
,
又∠AOB是直角,不改变,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-16-(-1+
 )÷3×[2-(-4)2]
)÷3×[2-(-4)2](2)解方程:
 -
-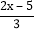 =-1
=-1(3)先化简,再求值:2(x2-2xy)+[2y2-3(x2-2xy+y2)+x2],其中x=1,y=-
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.

(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:ADBC=APBP;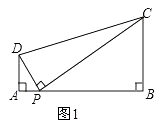
(2)探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.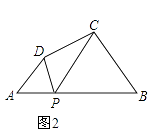
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A,设点P的运动时间为t(秒),当DC=4BC时,求t的值.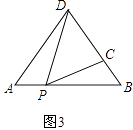
-
科目: 来源: 题型:
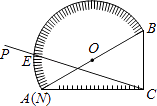
查看答案和解析>>【题目】如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应的读数是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有三个分别写有数字﹣1,0,1的乒乓球(形状,大小一样),先从盒子里随即取出一个乒乓球,记下数字后放回盒子,摇匀后再随即取出一个乒乓球,记下数字.
(1)请用树状图或列表的方法求两次取出乒乓球上数字相同的概率;
(2)求两次取出乒乓球上数字之积等于0的概率.
相关试题

