【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)详见解析;(3)符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
【解析】
试题分析:(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式;(2)先求出点A,B,C,D,E的坐标,从而求出BC=3![]() ,BE=2
,BE=2![]() ,CE=
,CE=![]() ,OD=1,OB=3,BD=
,OD=1,OB=3,BD=![]() ,求出比值,得到
,求出比值,得到![]() 得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
得出结论;(3)设出点P的坐标,表示出PB,PC,求出BC,分三种情况计算即可.
试题解析:(1)∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3,
(2)由(1)知,抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴E(1,﹣4),
∵B(3,0),A(﹣1,0),C(0,﹣3),
∴BC=3![]() ,BE=2
,BE=2![]() ,CE=
,CE=![]() ,
,
∵直线y=﹣![]() x+1与y轴交于点D,
x+1与y轴交于点D,
∴D(0,1),
∵B(3,0),
∴OD=1,OB=3,BD=![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴△BCE∽△BDO,
(3)存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴![]() =
=![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3![]() =
=![]() ,
,
∴m=±![]() ,
,
∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() ),
),
③当PC=BC时,
∴3![]() =
=![]() ,
,
∴m=﹣3±![]() ,
,
∴P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
考点:二次函数的综合题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2(x﹣3)2﹣4的最小值为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2+2a+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m2﹣m)x2+(m﹣1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
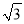 ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ,交OB于E点.
,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
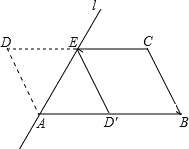
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2的图象向右平移2个单位,得到新的函数图像的表达式是( )
A. y=x2-2 B. y=(x-2)2 C. y=x2+2 D. y=(x+2)2
相关试题

