[题目]美丽的赤城湖水库是蓬溪县“天蓝水绿山青的真实写照.如图.赤城湖水库的大坝横截面是一个梯形.坝顶宽CD=4m.坝高3m.斜坡AD的坡度为1:2.5.斜坡BC的坡度为1:1.5.若大坝长200m.求大坝所用的土方是多少? 题目和参考答案 ——青夏教育精英家教网—

【题目】美丽的赤城湖水库是蓬溪县“天蓝水绿山青”的真实写照.如图，赤城湖水库的大坝横截面是一个梯形，坝顶宽CD=4m，坝高3m，斜坡AD的坡度为1:2.5，斜坡BC的坡度为1:1.5，若大坝长200m，求大坝所用的土方是多少？

参考答案：

【答案】6000m3

【解析】试题分析：过点D，C分别向AB作垂线，先求梯形的面积，进而求其所用的土方，即我们所说的容积即可．

试题解析：如图所示，过点D，C分别向AB作垂线，垂足分别为E，F，

∵DE：AE=1：2.5，DE=3，∴AE=7.5

∵CF：BF=1：1.5，∴BF=4.5

∴AB=7.5+4+4.5=16

∴S=×（16+4）×3=30m2，

∵大坝长200m，

∴所需土方6000m3．

答：这个大坝所用的土方是6000m3．

相关试题

科目： 来源： 题型：

【题目】阅读下面材料：
小明在数学课外小组活动时遇到这样一个问题：
如果一个不等式中含有绝对值，并且绝对值符号中含有未知数，我们把这个不等式叫做绝对值不等式，求绝对值不等式|x|＞3的解集．
小明同学的思路如下：
先根据绝对值的定义，求出|x|恰好是3时x的值，并在数轴上表示为点A，B，如图所示．观察数轴发现，以点A，B为分界点把数轴分为三部分：
点A左边的点表示的数的绝对值大于3；
点A，B之间的点表示的数的绝对值小于3；
点B右边的点表示的数的绝对值大于3．
因此，小明得出结论绝对值不等式|x|＞3的解集为：x＜-3或x＞3．
参照小明的思路，解决下列问题：
（1）请你直接写出下列绝对值不等式的解集．
①|x|＞1的解集是．
②|x|＜2.5的解集是．
（2）求绝对值不等式2|x-3|+5＞13的解集．
（3）直接写出不等式x2＞4的解集是 .
查看答案和解析>>
科目： 来源： 题型：

【题目】定义：至少有一组对边相等的四边形为“等对边四边形”．
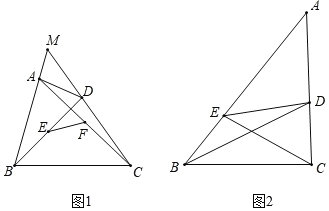
（1）请写出一个你学过的特殊四边形中是“等对边四边形”的名称；
（2）如图1，四边形ABCD是“等对边四边形”，其中AB=CD，边BA与CD的延长线交于点M，点E、F是对角线AC、BD的中点，若∠M=60°，求证：EFAB；
（3）如图2．在△ABC中，点D、E分别在边AC、AB上，且满足∠DBC=∠ECB∠A，线段CE、BD交于点．
①求证：∠BDC=∠AEC；
②请在图中找到一个“等对边四边形”，并给出证明．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在平面直角坐标系xOy中，一次函数y=x+1与x、y 轴分别交于点A、B，在直线 AB上截取BB1=AB，过点B1分别作x、y 轴的垂线，垂足分别为点A1、C1，得到矩形OA1B1C1；在直线 AB上截取B1B2= BB1，过点B2分别作x、y 轴的垂线，垂足分别为点A2 、C2，得到矩形OA2B2C2；在直线AB上截取B2B3= B1B2，过点B3分别作x、y 轴的垂线，垂足分别为点A3、C3，得到矩形OA3B3C3；……；
则点B1的坐标是；第3个矩形OA3B3C3的面积是；
第n个矩形OAnBnCn的面积是（用含n的式子表示，n是正整数）．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点，第二次点跳动至点第三次点跳动至点，第四次点跳动至点……，依此规律跳动下去，则点与点之间的距离是（）
A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目： 来源： 题型：

【题目】阅读下述材料：
我们在学习二次根式时，熟悉的分母有理化以及应用．其实，有一个类似的方法叫做“分子有理化”:
与分母有理化类似，分母和分子都乘以分子的有理化因式，从而消掉分子中的根式比如：
分子有理化可以用来比较某些二次根式的大小，也可以用来处理一些二次根式的最值问题．例如：
比较和的大小．可以先将它们分子有理化如下：

因为，所以
再例如：求的最大值．做法如下：
解：由可知，而
当时，分母有最小值2，所以的最大值是2．
解决下述问题：
（1）比较和的大小；
（2）求的最大值和最小值．
查看答案和解析>>
科目： 来源： 题型：

【题目】已知x1，x2 是关于x的方程（x－2）（x－m）=（p－2）（p－m）的两个实数根．
（1）求x1，x2 的值；
（2）若x1，x2 是某直角三角形的两直角边的长，问当实数m，p满足什么条件时，此直角三角形的面积最大？并求出其最大值．
查看答案和解析>>