【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
![]()
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论绝对值不等式|x|>3的解集为:x<-3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 .
②|x|<2.5的解集是 .
(2)求绝对值不等式2|x-3|+5>13的解集.
(3)直接写出不等式x2>4的解集是 .
参考答案:
【答案】(1)①x>1或x<-1;②-2.5<x<2.5;(2)x>7或x<-1;(3)x>2或x<-2.
【解析】
(1)先根据绝对值的定义,当|x|=1时,x=1或-1.再根据题意即可得;
(2)将2|x-3|+5>13化为|x-3|>4后,求出当|x-3|=4时,x=7或-1根据以上结论即可得;
(3)将x2>4化为|x|>2,再根据题意即可得.
解:(1)①根据绝对值的定义,当|x|=1时,x=1或-1,分界点把数轴分为三部分:
点-1左边的点表示的数的绝对值大于1;
点-1,1之间的点表示的数的绝对值小于1;
点1右边的点表示的数的绝对值大于1.
因此,绝对值不等式|x|>1的解集是 x>1或x<-1.
②根据绝对值的定义,当|x|=2.5时,x=2.5或-2.5,分界点把数轴分为三部分:
点-2.5左边的点表示的数的绝对值大于2.5;
点-2.5,2.5之间的点表示的数的绝对值小于2.5;
点2.5右边的点表示的数的绝对值大于2.5.
因此,绝对值不等式|x|<2.5的解集是-2.5<x<2.5.
故答案是:①x>1或x<-1;②-2.5<x<2.5;
(2)2|x-3|+5>13
∴2|x-3|>8
∴|x-3|>4
根据绝对值的定义,当|x-3|=4时,x=7或-1,分界点把数轴分为三部分:
点-1左边的点表示的数与3的差的绝对值大于4;
点-1,7之间的点表示的数与3的差的绝对值小于4;
点7右边的点表示的数与3的差的绝对值大于4
∴|x-3|>4的解集为x>7或x<-1;
∴2|x-3|+5>13的解集为x>7或x<-1;
(3)∵x2>4
∴|x|>2
根据绝对值的定义,当|x|=2时,x=2或-2,分界点把数轴分为三部分:
点-2左边的点表示的数的绝对值大于2;
点-2,2之间的点表示的数的绝对值小于2;
点2右边的点表示的数的绝对值大于2.
因此,绝对值不等式|x|>2的解集是 x>2或x<-2.
∴不等式x2>4的解集是 x>2或x<-2.
故答案是:x>2或x<-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小正方形的边长为1.
(1)直接写出四边形ABCD的面积和周长;
(2)求证:∠BCD=90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.
(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
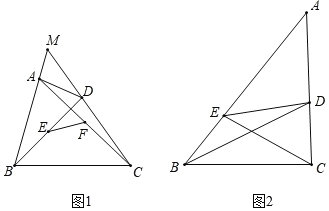
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF
 AB;
AB;(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB
 ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作x、y 轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线 AB上截取B1B2= BB1,过点B2分别作x、y 轴的垂线,垂足分别为点A2 、C2,得到矩形OA2B2C2;在直线AB上截取B2B3= B1B2,过点B3分别作x、y 轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;……;
则点B1的坐标是 ;第3个矩形OA3B3C3的面积是 ;
第n个矩形OAnBnCn的面积是 (用含n的式子表示,n是正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的赤城湖水库是蓬溪县“天蓝水绿山青”的真实写照.如图,赤城湖水库的大坝横截面是一个梯形,坝顶宽CD=4m,坝高3m,斜坡AD的坡度为1:2.5,斜坡BC的坡度为1:1.5,若大坝长200m,求大坝所用的土方是多少?

相关试题

