Question

【题目】如图，已知⊙O的弦AB等于半径，连接OB并延长使BC=OB．

（1）∠ABC=　 　．

（2）AC与⊙O有什么关系？请证明你的结论；

（3）在⊙O上，是否存在点D，使得AD=AC？若存在，请画出图形，并给出证明；若不存在，请说明理由．

Answer 1

【答案】（1）120°；（2）AC是⊙O的切线，证明见解析；（3）存在．证明见解析.

【解析】解：（１）１２０°；……………………………………………………………１分

（２）ＡＣ是⊙Ｏ的切线．……………………………………………………３分

证法一

∵ＡＢ＝ＯＢ＝ＯＡ，∴△ＯＡＢ为等边三角形，…………………………４分

∴∠ＯＢＡ＝∠ＡＯＢ＝６０°．……………………………………………５分

∵ＢＣ＝ＢＯ，∴ＢＣ＝ＢＡ，

∴∠Ｃ＝∠ＣＡＢ，……………………………………………………………６分

又∵∠ＯＢＡ＝∠Ｃ＋∠ＣＡＢ＝２∠Ｃ，

即２∠Ｃ＝６０°，∴∠Ｃ＝３０°，………………………………………７分

在△ＯＡＣ中，∵∠Ｏ＋∠Ｃ＝６０°＋３０°＝９０°，

∴∠ＯＡＣ＝９０°，…………………………………………………………８分

∴ＡＣ是⊙Ｏ的切线；

证法二：

∵ＢＣ＝ＯＢ，∴点Ｂ为边ＯＣ的中点，……………………………………４分

即ＡＢ为△ＯＡＣ的中位线，…………………………………………………５分

∵ＡＢ＝ＯＢ＝ＢＣ，即ＡＢ是边ＯＣ的一半，……………………………６分

∴△ＯＡＣ是以ＯＣ为斜边的直角三角形，…………………………………７分

∴∠ＯＡＣ＝９０°，…………………………………………………………８分

∴ＡＣ是⊙Ｏ的切线；

（３）存在．……………………………………………………………………９分

方法一：

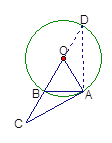
如图２，延长ＢＯ交⊙Ｏ于点Ｄ，即为所求的点．…………………………１０分

证明如下：

连结ＡＤ，∵ＢＤ为直径，∴∠ＤＡＢ＝９０°．…………………………１１分

在△ＣＡＯ和△ＤＡＢ中，

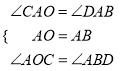∵，∴△ＣＡＯ≌△ＤＡＢ（ＡＳＡ），………………１２分

∴ＡＣ＝ＡＤ．…………………………………………………………………１３分

（也可由ＯＣ＝ＢＤ，根据ＡＡＳ证明；或ＨＬ证得，或证△ＡＢＣ≌△ＡＯＤ）

方法二：

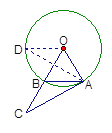
如图３，画∠ＡＯＤ＝１２０°，……………………………………………１０分

ＯＤ交⊙Ｏ于点Ｄ，即为所求的点．…………………………………………１１分

∵∠ＯＢＡ＝６０°，

∴∠ＡＢＣ＝１８０°－６０°＝１２０°．

在△ＡＯＤ和△ＡＢＣ中，

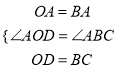∵，∴△ＡＯＤ≌△ＡＢＣ（ＳＡＳ），………………１２分

∴ＡＤ＝ＡＣ．…………………………………………………………………１３分

（１）由已知可知△AOB为等边三角形，利用平角求出∠ＡＢＣ的度数

（２）利用直角三角形的性质求出∠ＯＡＣ＝９０°，从而得出结论

（３）延长ＢＯ交⊙Ｏ于点Ｄ，即为所求的点，利用全等三角形求证