【题目】已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.

参考答案:
【答案】证明见解析
【解析】证法一:∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°.…………………………………………4分
在△ABE和△CDF中,……………………………………………………5分
∵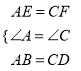 , ∴△ABE≌△CDF(SAS),……………………8分
, ∴△ABE≌△CDF(SAS),……………………8分
∴BE=DF(全等三角形对应边相等).…………………………………9分
证法二:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,…………………………………………………3分
又∵AE=CF,∴AD-AE=BC-CF,……………………………5分
即ED=BF,…………………………………………………………………6分
而ED∥BF,
∴四边形BFDE为平行四边形………………………………………………8分
∴BE=DF(平行四边形对边相等).……………………………………9分
利用全等三角形对应边相等求证
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-2y=-1,则代数式6-2x+4y的值为( )
A. 2
B. 4
C. 6
D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+(k﹣1)x+25是一个完全平方式,则常数k的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知空气的单位体积质量是0.001239g/cm3,则用科学记数法表示该数为( )
A. 1.239×10﹣3g/cm3 B. 1.239×10﹣2g/cm3
C. 0.1239×10﹣2g/cm3 D. 12.39×10﹣4g/cm3
-
科目: 来源: 题型:
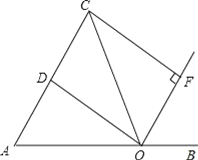
查看答案和解析>>【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在选拔2016年第十三届全国冬季运动会速滑运动员时,教练打算根据平时训练成绩,从运动员甲和乙种挑选1名成绩稳定的运动员,甲、乙两名运动员平时训练成绩的方差分别为S甲2=0.03,S乙2=0.20,你认为教练应该挑选的运动员是( )
A.乙
B.甲
C.甲、乙都行
D.无法判断 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5xy﹣(2x2﹣xy)+2(x2+3),其中x=1,y=﹣2.
相关试题

