【题目】如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.
⑴当t为何值时,△CPQ为直角三角形?
⑵求DE的长.
⑶取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C,PM,连接AC,,当t= 时,AC,的值最小,最小值为 .

参考答案:
【答案】(1)4;(2)6;(3)![]() ,
,![]()
【解析】
(1)由△ABC是等边三角形,可知∠C=60°,再由CQ=2CP列式即可求得t的值;
(2)过点Q作QF⊥AB交AB的延长线于F,易证△PEA≌△QFB(AAS),则EF=AB=12cm,易证△PED≌△QFD(AAS),DE=DF,即可求得DE=![]() EF=6;
EF=6;
(3)分析可知,点![]() 的轨迹为如图所示
的轨迹为如图所示![]() ,过点P作PN⊥MN,当A,
,过点P作PN⊥MN,当A,![]() ,M三点共线时,
,M三点共线时,![]() 有最小值,再根据等边三角形性质及直角三角形性质求解即可.
有最小值,再根据等边三角形性质及直角三角形性质求解即可.
解:(1)∵△ABC是等边三角形,
∴∠C=60°,
∴当CQ=2CP时,∠CPQ=90°,
∴12+t=2(12-t),
∴t=4,
∴t=4时,△CPQ是直角三角形.
(2)如图,过点Q作QF⊥AB交AB的延长线于F,
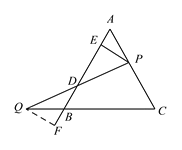
∵PE⊥AB,
∴∠PEA=∠F=90°,
∵PA=QB,∠A=∠ABC=∠QBF=60°,
∴△PEA≌△QFB(AAS),
∴AE=BF,
∴EF=AB=12cm,
∵∠PED=∠F=90°,∠PDE=∠QDF,PE=QF,
∴△PED≌△QFD(AAS),
∴DE=DF,
∴DE=![]() EF=6.
EF=6.
(3)分析可知,点![]() 的轨迹为如图所示
的轨迹为如图所示![]() ,过点P作PN⊥MN,
,过点P作PN⊥MN,
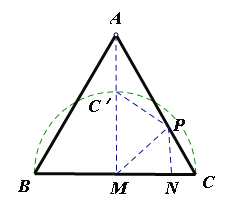
∴当A,![]() ,M三点共线时,
,M三点共线时,![]() 有最小值,
有最小值,
∵△ABC为等边三角形,M为BC中点,
∴AM⊥BC,∠ACM=60°,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
即当![]() 时,AC,的值最小,最小值为
时,AC,的值最小,最小值为![]() ,
,
故答案为:![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用2000元购进医用口罩若干个,第二次又用2000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个.
⑴求第一次和第二次分别购进的医用口罩数量为多少个?
⑵药店第一次购进口罩后,先以每个3元的价格出售,卖出了a个后购进第二批同款罩,由于进价提高了,药店将口罩的售价也提升至每个3.5元继续销售卖出了b个后,两次共收入4800元.因当地医院医疗物资紧缺,药店决定将剩余的口罩全部捐赠给医院.请问药店捐赠口罩至少有多少个?
-
科目: 来源: 题型:
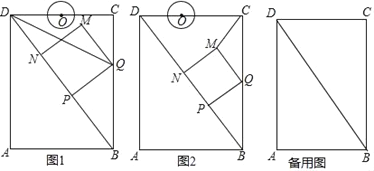
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤
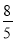 ).
).(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=
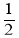 EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过平行四边形ABCD对角线的交点O,交AD于E,交BC于F,若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为_____.

-
科目: 来源: 题型:
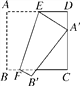
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.
相关试题

