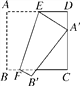
【题目】如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.
参考答案:
【答案】![]()
【解析】过点F作FG⊥AD,垂足为G,连接AA′,在△GEF中,由勾股定理可求得EG=5,轴对称的性质可知AA′⊥EF,由同角的余角相等可证明∠EAH=∠GFE,从而可证明△ADA′≌△FGE,故此可知GE=DA′=5,最后在△EDA′利用勾股定理列方程求解即可.
解:过点F作FG⊥AD,垂足为G,连接AA′.
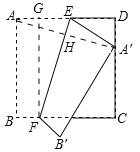
在Rt△EFG中,EG=![]() ,
,
∵轴对称的性质可知AA′⊥EF,
∴∠EAH+∠AEH=90.
∵FG⊥AD,
∴∠GEF+∠EFG=90.
∴∠DAA′=∠GFE.
在△GEF和△DA′A中,
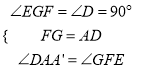 ,
,
∴△GEF≌△DA′A.
∴DA′=EG=5.
设AE=x,由翻折的性质可知EA′=x,则DE=12x.
在Rt△EDA′中,由勾股定理得:A′E2=DE2+A′D2,即x2=(12x)2+52.
解得:x=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.
⑴当t为何值时,△CPQ为直角三角形?
⑵求DE的长.
⑶取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C,PM,连接AC,,当t= 时,AC,的值最小,最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=
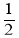 EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF过平行四边形ABCD对角线的交点O,交AD于E,交BC于F,若平行四边形ABCD的周长为18,OE=1.5,则四边形EFCD的周长为_____.

-
科目: 来源: 题型:
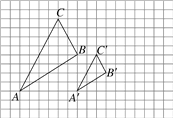
查看答案和解析>>【题目】如图,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
(1)画出位似中心O;
(2)△ABC与△A′B′C′的相似比为__________,面积比为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份

1
2
3
4
5
6
7
8
9
10
11
12
价格
 (元/千克)
(元/千克)5.00
5.50
5.00
4.80
2.00
1.50
1.00
0.90
1.50
3.00
2.50
3.50
A.
 是自变量,
是自变量, 是因变量
是因变量B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB运动,速度为2cm/s;动点Q从点B开始沿BC运动,速度为4cm/s.设P、Q两点同时运动,运动时间为ts(0<t<4),当△QBP与△ABC相似时,求t的值.

相关试题

