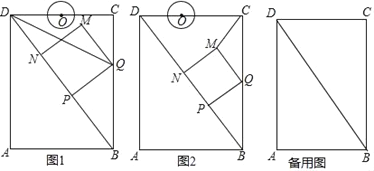
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
参考答案:
【答案】(1)1s; (2)S=﹣![]() t2+
t2+![]() t;(3)
t;(3)![]() .
.
【解析】试题分析:(1)由△DQC≌△DQP,推出DP=DC=6,在Rt△ADB中,BD=10,推出PB=4即可解决问题;
(2)过点M作MH⊥BC于点H,证明△HMQ∽△PQB,,由![]() =
=![]() ,得MH=
,得MH=![]() t,即可求得△CMQ的面积;
t,即可求得△CMQ的面积;
(3)设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,可证得△DFO∽△DCB,
由此![]() 即可解得:t值.
即可解得:t值.
试题解析:(1)∵四边形ABCD为矩形,
∴AB=CD=6cm、AD=BC=8cm,
则DB=10cm,
∵四边形PQMN为正方形,
∴∠BPQ=∠C=90°,
∵∠PBQ=∠CBD,
∴△BPQ∽△BCD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
则BQ=5t、PQ=3t,
∴CQ=BC﹣BQ=8﹣5t,
∵DQ平分∠BDC,
∴QP=QC,即3t=8﹣5t,
解得:t=1,
故答案为:1;
(2)如图a,过点M作MH⊥BC于点H,
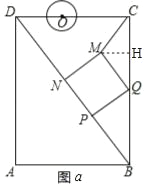
∴∠MHQ=∠QPB=∠MQP=90°,
则∠HMQ+∠HQM=∠PQB+∠HQM=90°,
∴∠HMQ=∠PQB,
∴△HMQ∽△PQB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
则MH=![]() t,
t,
∴S=![]() ×(8﹣5t)
×(8﹣5t)![]() t=﹣
t=﹣![]() t2+
t2+![]() t;
t;
(3)如图b,设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,
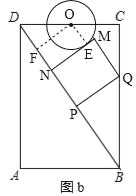
则四边形OENF为矩形,
∴OE=FN=1,∠DFO=∠C=90°,
∵∠FDO=∠CDB,
∴△DFO∽△DCB,
∴![]() ,即
,即![]() ,
,
解得:t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=
 x+
x+ 与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).⑴a= ,k= ;
⑵直接写出关于x的不等式
 x+
x+ ≥kx>0的解集 ;
≥kx>0的解集 ;⑶若点B在x轴上,MB=MA,直接写出点B的坐标 .
⑷在x轴上是否存在一点N,使得NM-NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:对于一些次数较高或者是比较复杂的式子进行因式分解时,换元法是一种常用的方法,下面是某同学用换元法对多项式
 进行因式分解的过程.
进行因式分解的过程.解:设

原式
 (第一步)
(第一步) (第二步)
(第二步) (第三步)
(第三步) (第四步)
(第四步)回答下列问题:
(1)该同学第二步到第三步运用了因式分解的__________(填代号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)按照“因式分解,必须进行到每一个多项式因式都不能再分解为止”的要求,该多项式分解因式的最后结果为______________.
(3)请你模仿以上方法对多项式
 进行因式分解.
进行因式分解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在防疫新冠状病毒期间,市民对医用口罩的需求越来越大.某药店第一次用2000元购进医用口罩若干个,第二次又用2000元购进该款口罩,但第二次每个口罩的进价是第一次进价的1.25倍,购进的数量比第一次少200个.
⑴求第一次和第二次分别购进的医用口罩数量为多少个?
⑵药店第一次购进口罩后,先以每个3元的价格出售,卖出了a个后购进第二批同款罩,由于进价提高了,药店将口罩的售价也提升至每个3.5元继续销售卖出了b个后,两次共收入4800元.因当地医院医疗物资紧缺,药店决定将剩余的口罩全部捐赠给医院.请问药店捐赠口罩至少有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AB=12cm,动点P从点A出发以1cm/s的速度沿AC匀速运动,动点Q同时从点B出发以同样的速度沿CB的延长线方向匀速运动,当点P到达点C时,点P,Q同时停止运动.设运动时间为ts,过点P作PE⊥AB于点E,连接PQ交AB于点D.
⑴当t为何值时,△CPQ为直角三角形?
⑵求DE的长.
⑶取线段BC的中点M,连接PM,将△CPM沿直线PM翻折,得到△C,PM,连接AC,,当t= 时,AC,的值最小,最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH=
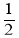 EG;④S△EFD=S△CEG成立的个数有( )
EG;④S△EFD=S△CEG成立的个数有( )
A.1个B.2个C.3个D.4个
相关试题

