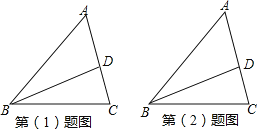
【题目】如图,已知BD为△ABC的角平分线请按如下要求操作与解答:
(1)过点D画DE∥BC交AB于点E.若∠A=68°,∠AED=42°,求△BCD各内角的度数;
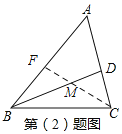
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,请找出图中所有与∠A相等的角,并说明理由.
参考答案:
【答案】(1) ∠DBC =21°,∠C =70°,∠BDC =89°;(2) ∠A=∠BMF=∠CMD=60°.
【解析】
(1)由DE∥BC可知∠AED=∠ABC=42°,根据角平分线的定义可得∠DBC=![]() ∠ABC=21°,根据三角形的内角和定理求得∠C和∠BDC的度数即可;(2)因为∠A=60°,根据三角形的内角和定理可得∠ABC+∠ACB=120°,由于BD平分∠ABC,CF平分∠ACB,可得∠MBC+∠MCB=60°,所以∠BMC=120°,由邻补角的定义可得∠BMF=∠CMD=60°.
∠ABC=21°,根据三角形的内角和定理求得∠C和∠BDC的度数即可;(2)因为∠A=60°,根据三角形的内角和定理可得∠ABC+∠ACB=120°,由于BD平分∠ABC,CF平分∠ACB,可得∠MBC+∠MCB=60°,所以∠BMC=120°,由邻补角的定义可得∠BMF=∠CMD=60°.
解:(1)过点D作DE∥BC交AB于点E,

∵DE∥BC,
∴∠AED=∠ABC=42°,
∵BD平分∠ABC,
∴∠DBC=![]() ∠ABC=21°,
∠ABC=21°,
∴∠C=180°-∠ABC-∠A=70°,
∴∠BDC=180°-∠DBC-∠C=89°.
(2)作△ABC的角平分线CF交BD于点M,
∵∠A=60°,
∴∠ABC+∠ACB=120°,
∴BD平分∠ABC,CF平分∠ACB,
∴∠MBC+∠MCB=![]() (∠ABC+∠ACB)=60°,
(∠ABC+∠ACB)=60°,
∴∠BMC=120°,
∴∠BMF=∠CMD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).

(1)点C的坐标是;
(2)将△ABC沿x轴正方向平移得到△A′B′C′,且B,C两点的对应点B′,C′恰好落在反比例函数y=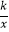 的图象上,求该反比例函数的解析式.
的图象上,求该反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是全面调查 B. 样本容量是360
C. 该校只有360个家长持反对态度 D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
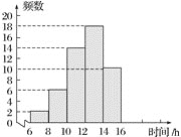
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12~14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8 h的大约有26人
-
科目: 来源: 题型:
查看答案和解析>>【题目】服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.

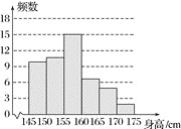
(1)表中m=________,n=________;
(2)身高x满足160≤x<170的校服记为L号,则需要订购L号校服的学生占被调查学生的百分数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
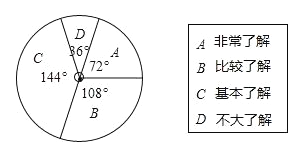
(1)求“非常了解”的人数的百分比.
(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.
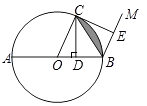
(1)当∠COB=60°时,直接写出阴影部分的面积;
(2)求证:CE是⊙O的切线.
相关试题

