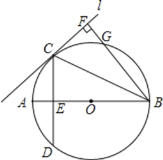
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
参考答案:
【答案】(1)见解析;(2)20.
【解析】
(1)观察图象知:只有FG的长度与AE相当,可猜想AE=FG,然后着手证明它们相等;求简单的线段相等,通常是证线段所在的三角形全等,那么本题需要构造全等三角形,连接AC、CG,然后证△AEC≌△GCF;连接BD,由于弧AC=弧AD,那么BA⊥CD,根据垂径定理知∠D=∠BCE;由弦切角定理知∠FCB=∠D=∠DCB,那么它们的余角也相等,即∠FBC=∠EBC,那么弧CG=弧AC,即AC=CG,再由角平分线的性质得CF=CE,根据HL即可判定所求的两个三角形全等,由此得证.
(2)由弦切角定理知∠FCG=∠FBC,它们的正弦值也相等,即可在Rt△FCG中,求得CG的长,也就得到了AC的长,在Rt△ACB中,CE⊥AB,由射影定理即可得到AB的长.
解:(1)FG=AE,理由如下:
连接CG、AC、BD;
∵![]() ,
,
∴BA⊥CD,
∴![]() ,即∠D=∠BCD;
,即∠D=∠BCD;
∵直线L切⊙O于C,
∴∠BCF=∠D=∠BCD,
∴∠FBC=∠ABC,
∴![]() ,CE=CF;
,CE=CF;
∴AC=CG;
△ACE和△GCF中,AC=CG、CE=CF,∠AEC=∠CFG=90°,
∴Rt△AEC≌Rt△GCF,则AE=FG.
(2)∵FC切⊙O于C,
∴∠FCG=∠FBC,即sin∠FCG=sin∠CBF=![]() ;
;
在Rt△FCG中,FG=AE=4,CG=FG÷sin∠FCG=4![]() ;
;
∴AC=CG=4![]() ;
;
在Rt△ABC中,CE⊥AB,由射影定理得:
AC2=AEAB,即AB=AC2÷AE=20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,C在BF上,
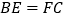 ,
,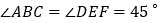 ,
,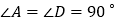 .
. 求证:
求证: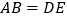 ;
;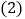 若AC交DE于M,且
若AC交DE于M,且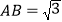 ,
,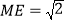 ,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角
,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角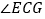 的度数.
的度数.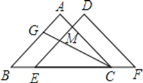
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
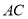 平分
平分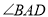 ,
, 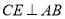 于
于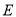 ,
, 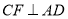 于
于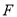 ,且
,且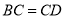 .
.(
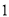 )求证:
)求证: 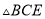 ≌
≌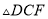 .
.(
 )若
)若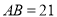 ,
, 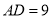 ,
, 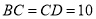 ,求
,求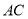 的长.
的长.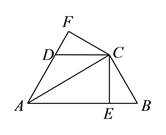
-
科目: 来源: 题型:
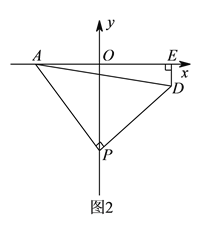
查看答案和解析>>【题目】如图
 ,
, 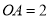 ,
,  ,以
,以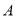 点为顶点、
点为顶点、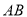 为腰在第三象限作等腰
为腰在第三象限作等腰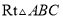 .
.(
 )求
)求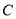 点的坐标.
点的坐标.(
 )如图
)如图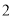 ,
, 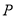 为
为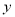 轴负半轴上一个动点,当
轴负半轴上一个动点,当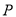 点沿
点沿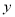 轴负半轴向下运动时,以
轴负半轴向下运动时,以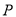 为顶点,
为顶点, 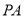 为腰作等腰
为腰作等腰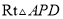 ,过
,过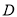 作
作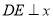 轴于
轴于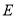 点,求
点,求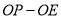 的值.
的值.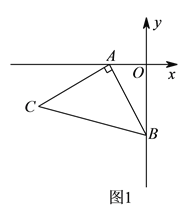
-
科目: 来源: 题型:
查看答案和解析>>【题目】“WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.
(1)求2016年平均每公顷水稻产量比2015年增加的百分数;
(2)求2015年这种水稻总产量比上年增加的百分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点.
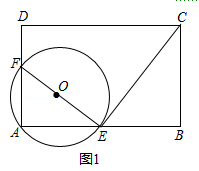
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值;
(3)如图2.若EF=EC且圈O与边CD相切,求n的值.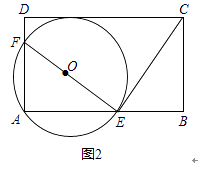
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠AOB=100°,∠BOD=60°,∠AOC=70°时,则∠COD=_____°(自己画图并计算)
相关试题

