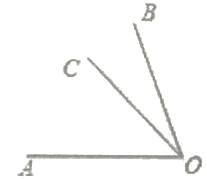
【题目】若∠AOB=100°,∠BOD=60°,∠AOC=70°时,则∠COD=_____°(自己画图并计算)
参考答案:
【答案】30°或90°或 110°或 130.
【解析】
分四种情况讨论图形的位置,然后根据∠AOB=100°,∠AOC=70°,∠BOD=60°,即可求解.
解:如图①∵∠AOB=100°,∠BOD=60°,∠AOC=70°,
∴∠COD=∠BOC+∠BOD=∠AOB﹣∠AOC+∠BOD=100°﹣70°+60°=90°;
如图②∠COD=360°﹣∠AOB﹣∠BOD﹣∠AOC=360°﹣100°﹣60°﹣70°=130°;
如图③∠COD=∠AOD+∠AOC=∠AOB﹣∠BOD+∠AOC=100°﹣60°+70°=110°;
如图④,∠COD=∠AOC+∠BOD﹣∠AOB=70°+60°﹣100°=30°;
故答案为:30°或90°或 110°或 130.

-
科目: 来源: 题型:
查看答案和解析>>【题目】题目:在同一平面上,若∠AOB=75°,∠BOC=15°,求∠AOC的度数.
下面是七(2)班马小虎同学的解题过程:
解:根据题意画出图形,如图所示,
∵∠AOC=∠AOB-∠BOC=75°-75°=60°
∴∠AOC=60°
若你是老师,会判马小虎满分吗?若会,说明理由;若不会,请指出错误之处,并给出你认为正确的解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线y=x+1与抛物线y=2x2相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
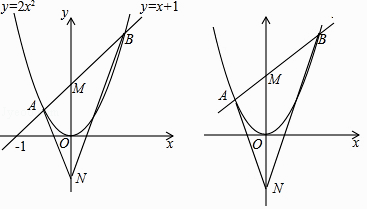
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线y=2x2变为y=ax2(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
- 四边形ABCD是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间
(小时)2
2.5
3
3.5
4
学生人数(名)
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8
B.中位数是3
C.平均数是3
D.方差是0.34 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( )
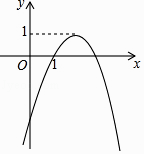
A.a<0,b<0,c>0
B.﹣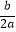 =1
=1
C.a+b+c<0
D.关于x的方程x2+bx+c=﹣1有两个不相等的实数根
相关试题

