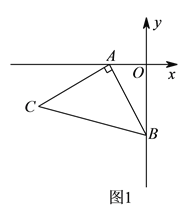
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]()
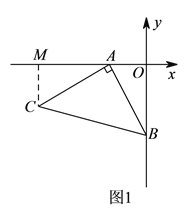
【解析】试题分析:(1)如图1,过C作CM⊥x轴于M点,则可以求出△MAC≌△OBA,可得CM=OA=2,MA=OB=4,即可得到结论;
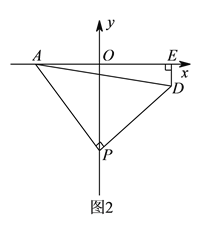
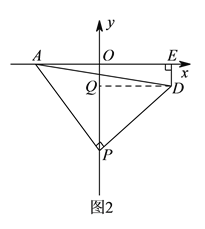
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,利用三角形全等的判定定理可得△AOP≌△PQD,进一步可得PQ=OA=2,即OP-DE=2.
试题解析:解:(1)如图1,过C作CM⊥x轴于M点.
∵∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,∴∠MAC=∠OBA.
在△MAC和△OBA中,∵∠CMA=∠AOB=90°,∠MAC=∠OBA,AC=AB,
∴△MAC≌△OBA(AAS),∴CM=OA=2,MA=OB=4,∴OM=OA+AM=2+4=6,∴点C的坐标为(-6,-2).
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,∴OP-DE=OP-OQ=PQ.
∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP.
在△AOP和△PQD中,∵∠AOP=∠PQD=90°,∠OAP=∠QPD,AP=PD,∴△AOP≌△PQD(AAS),∴PQ=OA=2,即OP-DE=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,E是AB上的一点,且
,E是AB上的一点,且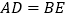 ,
,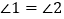 .
.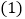 求证:
求证: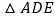 ≌
≌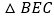 ;
;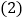 若
若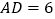 ,
,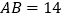 ,请求出CD的长.
,请求出CD的长.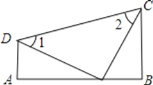
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,C在BF上,
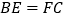 ,
,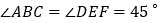 ,
,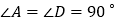 .
.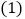 求证:
求证: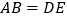 ;
;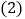 若AC交DE于M,且
若AC交DE于M,且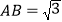 ,
,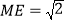 ,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角
,将线段CE绕点C顺时针旋转,使点E旋转到AB上的G处,求旋转角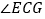 的度数.
的度数.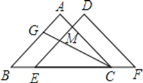
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
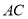 平分
平分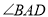 ,
, 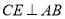 于
于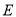 ,
, 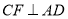 于
于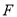 ,且
,且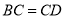 .
.(
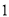 )求证:
)求证: 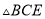 ≌
≌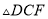 .
.(
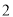 )若
)若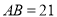 ,
, 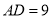 ,
, 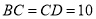 ,求
,求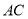 的长.
的长.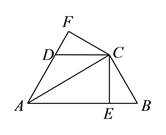
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB是
 的直径,直线L与
的直径,直线L与 相切于点C,
相切于点C, ,CD交AB于E,
,CD交AB于E, 直线L,垂足为F,BF交
直线L,垂足为F,BF交 于C.
于C. 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论; 若
若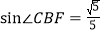 ,
, ,求AB的值.
,求AB的值.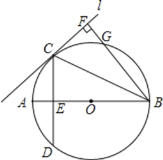
-
科目: 来源: 题型:
查看答案和解析>>【题目】“WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.
(1)求2016年平均每公顷水稻产量比2015年增加的百分数;
(2)求2015年这种水稻总产量比上年增加的百分数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与顶点A,B,D重合,∠AEF=∠BCE,圈O过A,E,F三点.
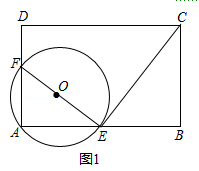
(1)求证:圈O与CE相切与点E;
(2)如图1,若AF=2FD且∠AEF=30°,求n的值;
(3)如图2.若EF=EC且圈O与边CD相切,求n的值.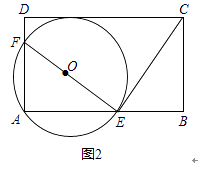
相关试题

