【题目】问题情境:
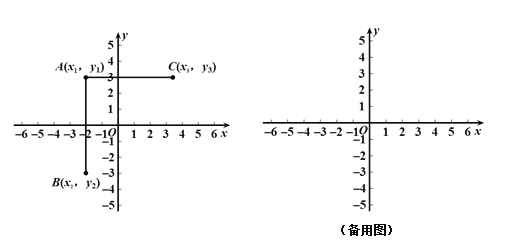
如图,在平面直角坐标系中有三点A(x1,y1),B(x2,y2),C(x3,y3),小明在学习中发现,当x1=x2,AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3,AC∥x轴,线段AC的长度为|x1﹣x3|.
初步应用
(1)若点A(﹣1,1)、B(2,1),则AB∥ 轴(填“x”或“y”);
(2)若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD= ;
(3)若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t= ;
拓展探索:
已知P(3,﹣3),PQ∥y轴.
(1)若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(2)若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.
参考答案:
【答案】初步应用:(1)x;(2)2;(3)-3;拓展探索:(1)Q点坐标为(3,-1)或(3,-5);(2)a﹣b=6.
【解析】
初步应用:(1)根据若![]() ,即可得出结论;
,即可得出结论;
(2)由C(1,﹣2),CD∥y轴,且点D在x轴上,可得D的坐标,再根据![]() 进行计算即可,
进行计算即可,
(3)由EF∥y轴,可得![]() ,从而可得答案,
,从而可得答案,
拓展探索:
(1)利用P(3,﹣3),PQ∥y轴,三角形OPQ的面积为3,可得![]() 的长度,结合
的长度,结合![]() 的位置直接得到答案,
的位置直接得到答案,
(2)利用P(3,﹣3),PQ∥y轴,PQ=a,写出![]() 的坐标,再根据平移规律得到
的坐标,再根据平移规律得到![]() 的坐标,利用
的坐标,利用![]() 的位置列方程得数量关系.
的位置列方程得数量关系.
解:(1)![]() A(﹣1,1)、B(2,1),
A(﹣1,1)、B(2,1),
![]() ,
,
![]() 轴,
轴,
故答案为:![]() .
.
(2)![]() C(1,﹣2),CD∥y轴,且点D在x轴上,
C(1,﹣2),CD∥y轴,且点D在x轴上,
![]() ,
,
![]()
故答案为:2.
(3)![]() EF∥y轴,
EF∥y轴,
![]()
![]() ,
,
![]() E(﹣3,2),点F(t,﹣4),
E(﹣3,2),点F(t,﹣4),
![]()
![]()
故答案为:![]()
拓展探索:
(1)如图:![]() P(3,﹣3),PQ∥y轴,
P(3,﹣3),PQ∥y轴,
![]()
![]()
![]() ,
,
同理:![]()
![]() .
.
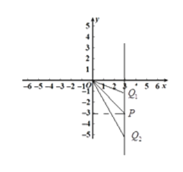
故答案为:(3,-1)或(3,-5)
(2)![]() PQ=a,P(3,﹣3),PQ∥y轴,
PQ=a,P(3,﹣3),PQ∥y轴,
![]() 或
或![]() (不合题意舍去)
(不合题意舍去)
![]() 往右平移
往右平移![]() 个单位长度后到点M,则
个单位长度后到点M,则![]() 坐标为
坐标为![]() ,
,
![]()
![]() 在第一象限的角平分线上,
在第一象限的角平分线上,
![]()
![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
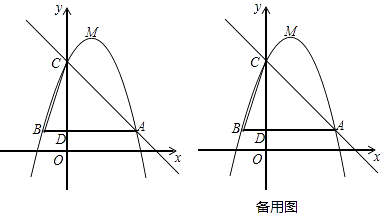
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P,A,M,M′为顶点的四边形为平行四边形时,直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'.
(1)AA'与CC'的位置关系为 ;
(2)求证:∠A'+∠CAC'+∠AC'C=180°;
(3)设
 ∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.
∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数;
(2)设∠BAD=θ,
①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.不论a为何值,函数图象必经过(2,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c表示△ABC的三边长,且满足
 +|a-12|+(b-13)2=0,则△ABC是( )
+|a-12|+(b-13)2=0,则△ABC是( )A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等边三角形
相关试题

