【题目】如图,已知二次函数y=﹣x2+bx+c(其中b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.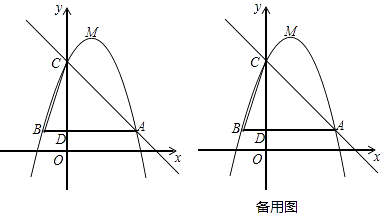
(1)求该二次函数的解析式及点M的坐标.
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围.
(3)沿直线AC方向平移该二次函数图象,使得CM与平移前的CB相等,求平移后点M的坐标.
(4)点P是直线AC上的动点,过点P作直线AC的垂线PQ,记点M关于直线PQ的对称点为M′.当以点P,A,M,M′为顶点的四边形为平行四边形时,直接写出点P的坐标.
参考答案:
【答案】
(1)解:把点A(3,1),点C(0,4)代入二次函数y=﹣x2+bx+c得 ![]()
解得 ![]() ,
,
∴二次函数解析式为y=﹣x2+2x+4,
配方得y=﹣(x﹣1)2+5,
∴点M的坐标为(1,5)
(2)解:设直线AC解析式为y=kx+b,把点A(3,1),C(0,4)代入得 ![]() ,
,
解得: ![]() ,
,
∴直线AC的解析式为y=﹣x+4,如图所示,对称轴直线x=1与△ABC两边分别交于点E、点F
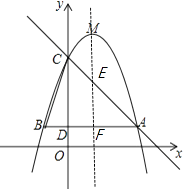
把x=1代入直线AC解析式y=﹣x+4解得y=3,则点E坐标为(1,3),点F坐标为(1,1),
点M向下平移m个单位后,坐标为(1,5﹣m),
由题意:1<5﹣m<3,解得2<m<4;
∴2<m<4
(3)解:如图,
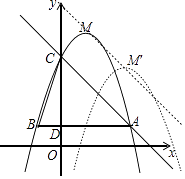
当y=1时,﹣x2+2x+4=1,解得x=﹣1或3,
∴B(﹣1,1),
∵C(0,4),
∴BC= ![]() =
= ![]() ,
,
∵MM′∥AC,CM′= ![]() ,M(1,5).
,M(1,5).
∴M′的坐标为(3,3)或(﹣1,7).
∴平移后点M的坐标(3,3)或(﹣1,7)
(4)解:如图,连接MC,MM′交PQ于F,则四边形CMFP是矩形,
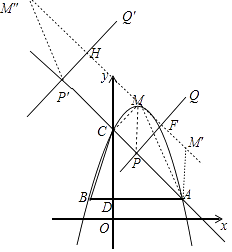
当四边形 PAM′M是平行四边形时,PA=MM′=2MF=2PC,设P(m,﹣m+4),
则有 ![]() (3﹣m)=2
(3﹣m)=2 ![]() m,
m,
∴m=1,
∴P(1,3),
当四边形 P′AMM′是平行四边形时,易知AP′=2CP′,
∴ ![]() (3﹣m)=2
(3﹣m)=2 ![]() (﹣m),
(﹣m),
解得m=﹣3,
∴P(﹣3,7),
综上所述,满足条件的点P的坐标为(1,3)或(﹣3,7).
【解析】(1)将点A(3,1),点C(0,4)代入二次函数y=﹣x2+bx+c,求出b、c的值即可,再用配方法求出顶点坐标。
(2)先求出直线AC的函数解析式,再根据已知AB∥x轴及点A的坐标,求出点E、F的坐标,点M向下平移m个单位后,坐标为(1,5﹣m),再见了不等式组,即可求出m的取值范围。
(3)当y=1时,﹣x2+2x+4=1,解方程求出方程的解,可得到点B的坐标,再Rt△BDC中,利用勾股定理可求出BC的长,由MM′∥AC及点M的坐标,就可求出平移后点M的坐标。
(4)连接MC,MM′交PQ于F,则四边形CMFP是矩形,当四边形 PAM′M是平行四边形时,PA=MM′=2MF=2PC,建立方程求出点P的坐标;当四边形 P′AMM′是平行四边形时,易知AP′=2CP′,建立方程求出点P的坐标。
【考点精析】关于本题考查的确定一次函数的表达式和勾股定理的概念,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
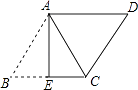
查看答案和解析>>【题目】如图,ABCD中,AB=13,AD=10,将ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
A.5
B.12
C.3
D.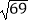
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
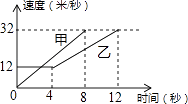
A.乙前4秒行驶的路程为48米
B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等
D.在4至8秒内甲的速度都大于乙的速度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
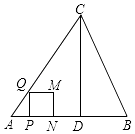
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'.
(1)AA'与CC'的位置关系为 ;
(2)求证:∠A'+∠CAC'+∠AC'C=180°;
(3)设
 ∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.
∠ACB=y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
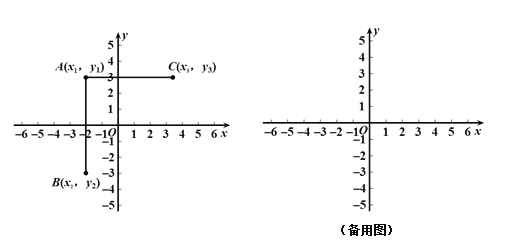
查看答案和解析>>【题目】问题情境:
如图,在平面直角坐标系中有三点A(x1,y1),B(x2,y2),C(x3,y3),小明在学习中发现,当x1=x2,AB∥y轴,线段AB的长度为|y1﹣y2|;当y1=y3,AC∥x轴,线段AC的长度为|x1﹣x3|.
初步应用
(1)若点A(﹣1,1)、B(2,1),则AB∥ 轴(填“x”或“y”);
(2)若点C(1,﹣2),CD∥y轴,且点D在x轴上,则CD= ;
(3)若点E(﹣3,2),点F(t,﹣4),且EF∥y轴,t= ;
拓展探索:
已知P(3,﹣3),PQ∥y轴.
(1)若三角形OPQ的面积为3,求满足条件的点Q的坐标.
(2)若PQ=a,将点Q向右平移b个单位长度到达点M,已知点M在第一象限角平分线上,请直接写出a,b之间满足的关系.
相关试题

