【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数;
(2)设∠BAD=θ,
①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.

参考答案:
【答案】(1)80°;(2)①10°,25°或40°;②5°或45°.
【解析】
试题分析:(1)由轴对称可以得出△ADB≌△ADF,就可以得出∠B=∠AFD,AB=AF,在证明△AGF≌△AGC就可以得出∠AFG=∠C,就可以求出∠DFG的值;
(2)①当GD=GF时,就可以得出∠GDF═80°,根据∠ADG=40+θ,就有40°+80°+40°+θ+θ=180°就可以求出结论;当DF=GF时,就可以得出∠GDF=50°,就有40°+50°+40°+2θ=180°,当DF=DG时,∠GDF=20°,就有40°+20°+40°+2θ=180°,从而求出结论;
②由已知条件可以得出∠DFG=80°,当∠GDF=90°时,就有40°+90°+40°+2θ=180°就可以求出结论,当∠DGF=90°时,就有∠GDF=10°,得出40°+10°+40°+2θ=180°求出结论.
试题解析:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,
∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,
∴AF=AC.
∵AG平分∠FAC,
∴∠FAG=∠CAG.
在△AGF和△AGC中,
AF=AC,∠FAG=∠CAG,AG=AG,
∴△AGF≌△AGC(SAS),
∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,
∴∠DFG=∠B+∠C=40°+40°=80°.
答:∠DFG的度数为80°;
(2)①当GD=GF时,
∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,
∴40°+80°+40°+θ+θ=180°,
∴θ=10°.
当DF=GF时,
∴∠FDG=∠FGD.
∵∠DFG=80°,
∴∠FDG=∠FGD=50°.
∴40°+50°+40°+2θ=180°,
∴θ=25°.
当DF=DG时,
∴∠DFG=∠DGF=80°,
∴∠GDF=20°,
∴40°+20°+40°+2θ=180°,
∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形;
②当∠GDF=90°时,
∵∠DFG=80°,
∴40°+90°+40°+2θ=180°,
∴θ=5°.
当∠DGF=90°时,
∵∠DFG=80°,
∴∠GDF=10°,
∴40°+10°+40°+2θ=180°,
∴θ=45°
∴当θ=5°或45°时,△DFG为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点P向下平移3个单位,向左平移2个单位后得到点Q(3,﹣1),则点P坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
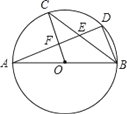
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)在ΔABC中,AB=AC
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示: _____________
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、C在反比例函数y=
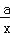 的图象上,点B,D在反比例函数y=
的图象上,点B,D在反比例函数y=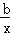 的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=
的图象上,a>b>0,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=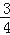 ,CD=
,CD=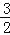 ,AB与CD间的距离为6,则a﹣b的值是 .
,AB与CD间的距离为6,则a﹣b的值是 .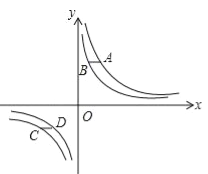
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程4x2+1=4x的根的情况是( )
A. 没有实数根 B. 只有一个实数根
C. 有两个相等的实数根 D. 有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子内装有大小、形状相同的四个球,其中红球1个、白球3个,小明从中随机摸出一个球后不放回,再摸出一个球,则事件“两次都摸到白球”是( )
A. 必然事件 B. 确定事件 C. 随机事件 D. 不可能事件
相关试题

