【题目】为倡导读书风尚,打造书香校园,学校计划购买一批图书。若同时购进![]() 种图书10本和
种图书10本和![]() 种图书7本,共需395元;若同时购进
种图书7本,共需395元;若同时购进![]() 种图书5本和
种图书5本和![]() 种图书3本,共需185元。
种图书3本,共需185元。
(1)求![]() 两种图书的单价各是多少元?
两种图书的单价各是多少元?
(2)若学校计划购买这两种图书共80本,要求每种都要购买,且![]() 种图书的数量少于
种图书的数量少于![]() 种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
参考答案:
【答案】(1)![]() 种图书单价22元,
种图书单价22元,![]() 种图书单价25元;(2)有三种方案
种图书单价25元;(2)有三种方案
【解析】
(1)设购买A种图书每本x元,则购买B种图书每本y元,根据购买A种图书10本、B种图书7本,共用了395元,再根据购买A种图书5本、B种图书3本,共用了185元列出方程组,求解即可;
(2)设购买A种图书m本,根据题意列出不等式解答即可.
(1)设![]() 种图书单价
种图书单价![]() 元,
元,![]() 种图书单价
种图书单价![]() 元,
元,
依题意,得![]() ,解得
,解得![]()
答:![]() 种图书单价22元,
种图书单价22元,![]() 种图书单价25元;
种图书单价25元;
(2)设购买![]() 种图书
种图书![]() 本,则购买
本,则购买![]() 种图书
种图书![]() 本
本
依题意得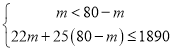
解得![]() ;
;
∵![]() 为正整数,
为正整数,
∴取![]()
∴共有三种方案,方案如下:
购买![]() 种图书37本,则购买
种图书37本,则购买![]() 种图书43本;
种图书43本;
购买![]() 种图书38本,则购买
种图书38本,则购买![]() 种图书42本;
种图书42本;
购买![]() 种图书39本,则购买
种图书39本,则购买![]() 种图书41本.
种图书41本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数
购买数量(件

购买总费用(元

A
B
第一次
2
1
55
第二次
1
3
65
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点 的坐标。
的坐标。(1)点
 在
在 轴上;
轴上;(2)点
 横坐标比纵坐标大3;
横坐标比纵坐标大3;(3)点
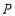 在过
在过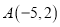 点,且与
点,且与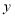 轴平行的直线上。
轴平行的直线上。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A.
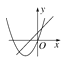 B.
B. 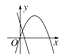 C.
C. 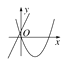 D.
D. 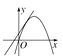
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:2x2﹣7x+6=0;
(2)已知:关于x的方程x2+kx﹣2=0.
①求证:方程有两个不相等的实数根;
②若方程的一个根是﹣1,求另一个根及k值.
相关试题

