【题目】(1)解方程:2x2﹣7x+6=0;
(2)已知:关于x的方程x2+kx﹣2=0.
①求证:方程有两个不相等的实数根;
②若方程的一个根是﹣1,求另一个根及k值.
参考答案:
【答案】(1)x1=2,x2= ![]() ;(2)①答案见解析;(2)k的值为﹣1,方程另一根为2.
;(2)①答案见解析;(2)k的值为﹣1,方程另一根为2.
【解析】试题分析:(1)利用求根公式进行求解即可得;
(2)①利用根据的判别式进行证明即可;
②先求出k的值,然后再解方程即可得.
试题解析:(1)∵2x2﹣7x+6=0,
∴a=2,b=﹣7,c=6,
∴△=(﹣7)2﹣4×2×6=1,
∴x=![]() ,
,
∴x1=2,x2= ![]() ;
;
(2)①∵x2+kx﹣2=0,
∴△=k2﹣4×(﹣2)=k2+8>0,
∴方程有两个不相等的实数根;
②∵方程的一个根是﹣1,
∴1﹣k﹣2=0,解得k=﹣1,
∴方程为x2﹣x﹣2=0,解得x=﹣1或x=2,
即k的值为﹣1,方程另一根为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导读书风尚,打造书香校园,学校计划购买一批图书。若同时购进
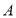 种图书10本和
种图书10本和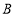 种图书7本,共需395元;若同时购进
种图书7本,共需395元;若同时购进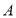 种图书5本和
种图书5本和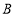 种图书3本,共需185元。
种图书3本,共需185元。(1)求
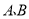 两种图书的单价各是多少元?
两种图书的单价各是多少元?(2)若学校计划购买这两种图书共80本,要求每种都要购买,且
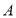 种图书的数量少于
种图书的数量少于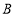 种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )
A.
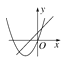 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
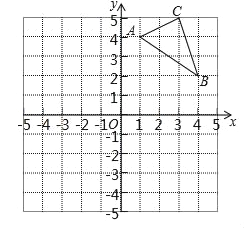
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个小方格的边长均为1个单位长度).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并求出点B旋转到点B2所经过的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式.
①4×1×2+1=(1+2)2;②4×2×3+1=(2+3)2;③4×3×4+1=(3+4)2…
(1)根据你观察、归纳,发现的规律,写出4×2016×2017+1可以是哪个数的平方?
(2)试猜想第n个等式,并通过计算验证它是否成立.
(3)利用前面的规律,将4(
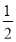 x2+x)(
x2+x)(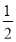 x2+x+1)+1因式分解.
x2+x+1)+1因式分解. -
科目: 来源: 题型:
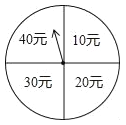
查看答案和解析>>【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
相关试题

