【题目】小明购买A,B两种商品,每次购买同一种商品的单价相同,具体信息如下表:
次数 | 购买数量(件 | 购买总费用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根据以上信息解答下列问题:
(1)求A,B两种商品的单价;
(2)若第三次购买这两种商品共12件,且A种商品的数量不少于B种商品数量的2倍,请设计出最省钱的购买方案,并说明理由.
参考答案:
【答案】(1)A种商品的单价为20元,B种商品的单价为15元;(2) 当a=8时所花钱数最少,即购买A商品8件,B商品4件.
【解析】
(1)列二元一次方程组,用代入法或加减法解方程即可;
(2)将题目转化为一元一次不等式,利用一元一次不等式解即可.
解:(1)设![]() 种商品的单价为
种商品的单价为![]() 元,
元,![]() 种商品的单价为
种商品的单价为![]() 元,根据题意可得:
元,根据题意可得:
![]() ,
,
解得:![]() ,
,
答:![]() 种商品的单价为20元,
种商品的单价为20元,![]() 种商品的单价为15元;
种商品的单价为15元;
(2)设第三次购买商品![]() 种
种![]() 件,则购买
件,则购买![]() 种商品
种商品![]() 件,根据题意可得:
件,根据题意可得:
![]() ,
,
得:![]() ,
,
![]()
![]() 当
当![]() 时所花钱数最少,即购买
时所花钱数最少,即购买![]() 商品8件,
商品8件,![]() 商品4件.
商品4件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
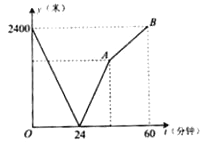
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
-
科目: 来源: 题型:
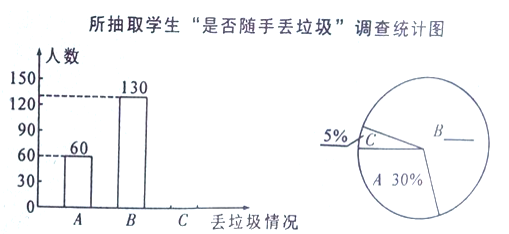
查看答案和解析>>【题目】“垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为:
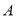 ——从不随手丢垃圾;
——从不随手丢垃圾;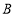 ——偶尔随手丢垃圾;
——偶尔随手丢垃圾;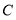 ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:(1)补全条形统计图和扇形统计图;
(2)图中“偶尔随手丢垃圾”所在扇形的圆心角为______________;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
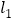 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且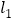 与x轴交于点D,直线
与x轴交于点D,直线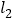 经过点A,B,直线
经过点A,B,直线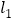 ,
,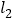 交于点C.
交于点C.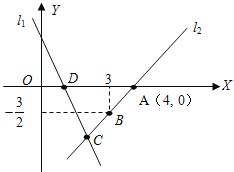
(1)求点D的坐标;
(2)求直线
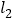 的解析表达式;
的解析表达式;(3)求△ADC的面积;
(4)在直线
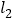 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
 ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点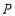 的坐标。
的坐标。(1)点
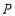 在
在 轴上;
轴上;(2)点
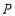 横坐标比纵坐标大3;
横坐标比纵坐标大3;(3)点
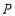 在过
在过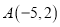 点,且与
点,且与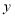 轴平行的直线上。
轴平行的直线上。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导读书风尚,打造书香校园,学校计划购买一批图书。若同时购进
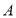 种图书10本和
种图书10本和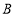 种图书7本,共需395元;若同时购进
种图书7本,共需395元;若同时购进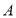 种图书5本和
种图书5本和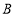 种图书3本,共需185元。
种图书3本,共需185元。(1)求
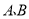 两种图书的单价各是多少元?
两种图书的单价各是多少元?(2)若学校计划购买这两种图书共80本,要求每种都要购买,且
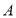 种图书的数量少于
种图书的数量少于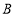 种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
相关试题

