【题目】某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
参考答案:
【答案】(1)装运乙种水果的车有2辆、丙种水果的汽车有6辆;(2)装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆;(3)当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.
【解析】(1)设装运乙、丙水果的车分别为x辆,y辆,得:![]() ,解得:
,解得:![]() .
.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆.
(2)设装运乙、丙水果的车分别为a辆,b辆,得:![]() ,解得:
,解得:![]() .
.
答:装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆.
(3)设总利润为w千元,w=4×5m+2×7(m﹣12)=4×3(32﹣2m)=10m+216.
∵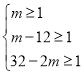 ,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
,∴13≤m≤15.5,∵m为正整数,∴m=13,14,15,在w=10m+216中,w随x的增大而增大,∴当m=15时,W最大=366(千元).
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个四边形的边长分别是a、b、c、d,其中a、c为对边,且a2+b2+c2+d2=2ac+2bd,则此四边形的形状为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A和点B相距60cm,且关于直线L对称,一只电动青蛙在与直线L相距20cm,与点A相距50cm的点P1处以A为对称中心跳至P2处,然后从P2处以L为对称轴跳至P3处,再从P3处以B为对称中心跳至P4处,再从P4处以L为对称轴跳至P5处,又从P5处以A为对称中心跳至P6处…,如此重复跳跃,则P2011与直线L的距离是( )
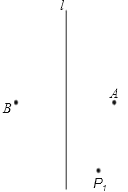
A.20cm
B.30cm
C.40cm
D.50cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个相似三角形的周长比是1:4,则他们的面积比为( )
A.1:4B.1:2C.2:1D.1:16
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边a、b、c满足条件a2+b2+c2+50=6a+8b+10c,试判断△ABC的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习中,小明发现:当a=-1,0,1时,a2-8a+20的值都是正数,于是小明猜想:当a为任意整数时,a2-8a+20的值都是正数,小明的猜想正确吗?简要说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )
A.直角三角形
B.等腰三角形
C.钝角三角形
D.锐角三角形
相关试题

