【题目】在学习中,小明发现:当a=-1,0,1时,a2-8a+20的值都是正数,于是小明猜想:当a为任意整数时,a2-8a+20的值都是正数,小明的猜想正确吗?简要说明你的理由.
参考答案:
【答案】解猜想正确,理由详见解析.
【解析】
首先配方,进而利用非负数的性质即可说明猜想正确.
解:解猜想正确.理由如下:
a2-8a+20═a2-8a+42+4=(a-4)2+4,因为(a-4)2≥0,
所以(a-4)2+4≥4,
所以当a为任意整数时,a2-8a+20的值都是正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个相似三角形的周长比是1:4,则他们的面积比为( )
A.1:4B.1:2C.2:1D.1:16
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边a、b、c满足条件a2+b2+c2+50=6a+8b+10c,试判断△ABC的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )
A.直角三角形
B.等腰三角形
C.钝角三角形
D.锐角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】检验方程后面的数是不是它的解.
2x+1=3x﹣1(x=﹣1,x=2) -
科目: 来源: 题型:
查看答案和解析>>【题目】
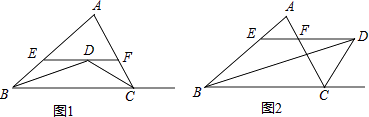
(1)如图1,在△ABC中,BD平分∠ABC,CD平分∠ACB.过D作EF∥BC交AB于E,交AC于F,请说明EF=BE+CF的理由.
(2)如图2,BD平分∠ABC,CD是△ABC中∠ACB的外角平分线,若仍然过点D作EF∥BC交AB于E,交AC于F,第(1)题的结论还成立吗?如果成立,请说明理由;如果不成立,你能否找到EF与BE、CF之间类似的数量关系?
相关试题

