【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离 ![]() ,
,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
参考答案:
【答案】
(1)解:∵A(2,4)、B(﹣3,﹣8),
∴AB= ![]() =13
=13
(2)解:∵A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,
∴AB=|4﹣(﹣1)|=5
(3)解:△DEF为等腰三角形,理由为:
∵D(1,6)、E(﹣2,2)、F(4,2),
∴DE= ![]() =5,DF=
=5,DF= ![]() =5,EF=
=5,EF= ![]() =6,即DE=DF,
=6,即DE=DF,
则△DEF为等腰三角形
(4)解:做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,

设直线DF′解析式为y=kx+b,
将D(1,6),F′(4,﹣2)代入得: ![]() ,
,
解得:  ,
,
∴直线DF′解析式为y=﹣ ![]() x+
x+ ![]() ,
,
令y=0,得:x= ![]() ,即P(
,即P( ![]() ,0),
,0),
∵PF=PF′,
∴PD+PF=DP+PF′=DF′= ![]() =
= ![]() ,
,
则PD+PF的长度最短时点P的坐标为( ![]() ,0),此时PD+PF的最短长度为
,0),此时PD+PF的最短长度为 ![]() .
.
【解析】(1)代入公式易得AB=![]() =13。
=13。
(2)由于A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,有公式易得AB=|4﹣(﹣1)|=5;
(3)由三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2)代入公式可得各点之间的距离,再利用勾股定理的逆定理可得三角形为直角三角形;
(4)做出F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,求得直线DF′解析式可得P点坐标,再利用公式可得PD+PF的最短长度为 ![]()
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时)
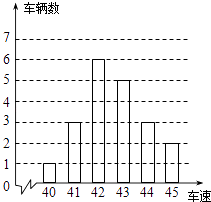
(1)车速的众数是多少?
(2)计算这些车辆的平均数度;
(3)车速的中位数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数m,n满足(m+n)2=9,(m﹣n)2=1,求下列各式的值.
(1)mn;
(2)m2+n2﹣mn. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,5)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种球形病毒的直径大约为0.000000101,则数0.000000101用科学记数法为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】深高北校区初二年级举行“名著知识竟赛”决赛.在这之前,初二(24)班举行了三轮初赛,为了从甲乙两名平均分最高的同学中选取一名发挥稳定的同学参加决赛,需要考察这两位同学三轮初赛成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
相关试题

