【题目】如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD= . 
参考答案:
【答案】5
【解析】解:∵OP平分∠AOB,
∴∠AOP=∠BOP,
∵PC∥OB,
∴∠CPO=∠BOP,∴∠CPO=∠AOP,
∴PC=OC,
∵PC=10,
∴OC=PC=10,
过P作PE⊥OA于点E, 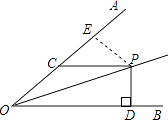
∵PD⊥OB,OP平分∠AOB,
∴PD=PE,
∵PC∥OB,∠AOB=30°
∴∠ECP=∠AOB=30°
在Rt△ECP中,PE= ![]() PC=5,
PC=5,
∴PD=PE=5,
故答案为:5.
由OP平分∠AOB和PC∥OB易得三角形OPC为等腰三角形OC=PC=10,再由OP平分∠AOB,角平线上的点到角的两边距离相等得PD=PE,又由PC∥OB,∠AOB=30°可得PD=PE=5。
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,5)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离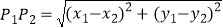 ,
,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种球形病毒的直径大约为0.000000101,则数0.000000101用科学记数法为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】深高北校区初二年级举行“名著知识竟赛”决赛.在这之前,初二(24)班举行了三轮初赛,为了从甲乙两名平均分最高的同学中选取一名发挥稳定的同学参加决赛,需要考察这两位同学三轮初赛成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解ax2-9a=.
-
科目: 来源: 题型:
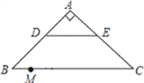
查看答案和解析>>【题目】如图,在Rt△ABC中.∠A=90°.AB=AC,BC=20,DE是△ABC的中位线.点M是边BC上一点.BM=3.点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是_____.
相关试题

