【题目】如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时)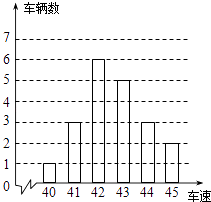
(1)车速的众数是多少?
(2)计算这些车辆的平均数度;
(3)车速的中位数是多少?
参考答案:
【答案】
(1)解:根据条形统计图所给出的数据得:42出现了6次,出现的次数最多,则车速的众数是42千米/时
(2)解:这些车辆的平均数度是:
(40+41×3+42×6+43×5+44×3+45×2)÷20=42.6(千米/时),
答:这些车辆的平均数度是42.6千米/时
(3)解:因为共有20辆车,中位数是第10和11个数的平均数,
所以中位数是42和43的平均数,
(42+43)÷2=42.5(千米/时),
所以车速的中位数是42.5千米/时
【解析】(1)出现的次数最多数据是众数,42出现了6次,易得众数为42千米/小时。
(2)加权平均数的计算注意各个数据的权。
(3)全部数据按从大到小排列,如果是奇数个数则最中间的数为中位数,如果是偶数个数,则最中间的两数的平均数为中位数。所以易得因为共有20辆车,中位数是第10和11个数的平均数所以中位数是42和43的平均数42.5千米/时。
【考点精析】本题主要考查了中位数、众数的相关知识点,需要掌握中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA.若﹣3am﹣1b2与anb2n﹣2是同类项且OA=m,OB=n,求出m和n的值以及点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解
(1)﹣2x2y+12xy﹣18y
(2)2x2y﹣8y. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a+2b=5abB. a3a2=a6C. a3÷a2=aD. (3a)2=3a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数m,n满足(m+n)2=9,(m﹣n)2=1,求下列各式的值.
(1)mn;
(2)m2+n2﹣mn. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,5)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离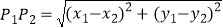 ,
,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
相关试题

