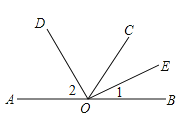
【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
参考答案:
【答案】(1)∠2=67°;(2)∠DOE的大小始终不变,等于90°;
【解析】
(1)由∠AOC与∠COB互补,且OD是∠AOC的平分线,OE是∠COB的平分线,利用角平分线定义及等式的性质求出∠2与∠1的度数之和,根据∠1的度数即可求出∠2的度数;
(2)∠DOE度数不变,度数为90度,理由为:根据∠AOC与∠COB互补,且OD是∠AOC的平分线,OE是∠COB的平分线,利用角平分线定义及等式的性质求出∠DOC与∠COE的度数之和为平角的一半,即可求出度数.
(1)∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠2=∠DOC,∠1=∠COE,
∵∠AOC+∠COB=180°,
∴∠2+∠COD+∠1+∠COE=2(∠1+∠2)=180°,
∴∠1+∠2=90°,
∵∠1=23°,
∴∠2=67°;
(2)∠DOE度数不变,度数为90°,理由为:
∵OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠2=∠DOC,∠1=∠COE,
∵∠AOC+∠COB=180°,
∴∠2+∠COD+∠1+∠COE=2(∠COD+∠COE)=180°,
∴∠COD+∠COE=90°,即∠DOE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算
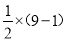 ,
, 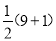 与
与 ,
,  并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
-
科目: 来源: 题型:
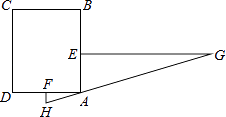
查看答案和解析>>【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OM是∠AOC的角平分线,ON是∠BOC的角平分线;
(1)当∠BOC=40°时,求∠MON的大小?
(2)当∠BOC的大小发生变化时,∠MON的大小是否发生改变?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
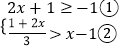 ,并把不等式组的解集在数轴上表示出来.
,并把不等式组的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1:
 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
相关试题

