【题目】据我国古代《周髀算经》记载,大约公元1120年,商高曾对周公说过一段话,其意思是将一根直尺折成一个直角,两端连接得一个直角三角形,如果勾是三,股是四,那么弦就等于五,后人概括为“勾三股四弦五”。
(1)观察:3,4,5; 5,12,13; 7,24,25……发现这些勾股数的勾都是奇数,且从3起就没有间断过。计算![]() ,
, ![]() 与
与![]() ,
, ![]() 并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
并根据发现的规律,分别写出能表示7,24,25的股和弦的算式;
(2)根据(1)的规律,用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦,合理猜想它们之间的两种相等关系并对其一种猜想加以说明。
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)勾、股、弦的算式为n,
;(2)勾、股、弦的算式为n, ![]() ,
, ![]()
两种相等关系为: ![]() ,
, ![]()
理由见解析
【解析】试题分析:(1)根据所提供的例子发现股是勾的平方减去1的二分之一,弦是勾的平方加1的二分之一;
(2)①:弦股=1;关系式②:勾2+股2=弦2.
试题解析:(1)∵![]()
∴7,24,25的股的算式为![]()
弦的算式为![]()
(2)当n为奇数且![]() ,勾、股、弦的代数式分别为:
,勾、股、弦的代数式分别为: ![]()
例如关系式①:弦股=1;关系式②:勾2+股2=弦2.
证明关系式①:弦股![]()
或证明关系式②:勾2+股2![]() =弦2.
=弦2.
∴猜想得证;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
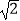 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ) 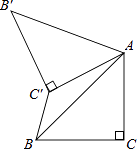
A.2﹣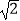
B.
C.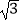 ﹣1
﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;

-
科目: 来源: 题型:
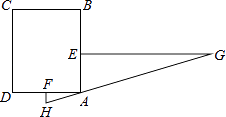
查看答案和解析>>【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF=______.

-
科目: 来源: 题型:
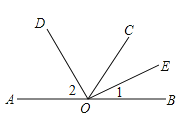
查看答案和解析>>【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
相关试题

