【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
参考答案:
【答案】解:过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵i= ![]() =
= ![]() =tan∠ECF,
=tan∠ECF,
∴∠ECF=30°,
∴EF= ![]() CE=10米,CF=10
CE=10米,CF=10 ![]() 米,
米,
∴BH=EF=10米,HE=BF=BC+CF=(25+10 ![]() )米,
)米,
在Rt△AHE中,∵∠HAE=45°,
∴AH=HE=(25+10 ![]() )米,
)米,
∴AB=AH+HB=(35+10 ![]() )米.
)米.
答:楼房AB的高为(35+10 ![]() )米.
)米.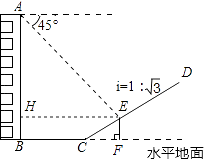
【解析】过点E作EF⊥BC的延长线于F,EH⊥AB于点H,根据CE=20米,坡度为i=1: ![]() ,分别求出EF、CF的长度,在Rt△AEH中求出AH,继而可得楼房AB的高.
,分别求出EF、CF的长度,在Rt△AEH中求出AH,继而可得楼房AB的高.
【考点精析】通过灵活运用关于坡度坡角问题和关于仰角俯角问题,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.
-
科目: 来源: 题型:
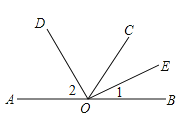
查看答案和解析>>【题目】如图,O是直线AB上的一点,C是直线AB外的一点,OD是∠AOC的平分线,
OE是∠COB的平分线.
(1)已知∠1=23°,求∠2的度数;
(2)无论点C的位置如何改变,图中是否存在一个角,它的大小始终不变(∠AOB除外)?如果存在,求出这个角的度数;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OM是∠AOC的角平分线,ON是∠BOC的角平分线;
(1)当∠BOC=40°时,求∠MON的大小?
(2)当∠BOC的大小发生变化时,∠MON的大小是否发生改变?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
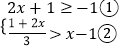 ,并把不等式组的解集在数轴上表示出来.
,并把不等式组的解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,已知格点△ABC和格点O.
(1)画出△ABC关于点O对称的△A′B′C′;
(2)若以点A、O、C、D为顶点的四边形是平行四边形,则点D的坐标为__.(写出所有可能的结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,从全国旅游景区质量等级评审会上传来喜讯,我市“风冈茶海之心”、“赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区.至此,全市“4A”级景区已达13个.某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,按答数多少分为熟悉(A),基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了一下两幅统计图(不完整),请根据图中信息解答以下各题:

(1)本次调查活动的样本容量是;
(2)调查中属于“基本了解”的市民有人;
(3)补全条形统计图;
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
相关试题

