【题目】在同一平面直角坐标系中，函数y＝ax2+bx与y＝﹣bx+a的图象可能是（　　）

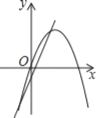A.B.C.D.

参考答案：

【答案】B

【解析】

首先根据图形中给出的一次函数图象确定a、b的符号，进而运用二次函数的性质判断图形中给出的二次函数的图象是否符合题意，根据选项逐一讨论解析，即可解决问题．

解：A、对于直线y=-bx+a来说，由图象可以判断，a＜0，b＞0；而对于抛物线y=ax2+bx来说，图象应开口向下，故不合题意；

B、对于直线y=-bx+a来说，由图象可以判断，a＞0，b＜0；而对于抛物线y=ax2+bx来说，图象开口向上，对称轴x=-＞0，在y轴的右侧，符合题意，图形正确；
C、对于直线y=-bx+a来说，由图象可以判断，a＜0，b＜0；而对于抛物线y=ax2+bx来说，对称轴x=-＜0，应位于y轴的左侧，故不合题意；
D、对于直线y=-bx+a来说，由图象可以判断，a＞0，b＜0；而对于抛物线y=ax2+bx来说，图象应开口向下，故不合题意．
故选：B．

关闭