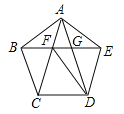
【题目】(2017山东省莱芜市)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】B
【解析】解:①∵五方形ABCDE是正五边形,∴AB=BC,∠ABC=180°﹣![]() =108°,∴∠BAC=∠ACB=36°,∴∠ACD=108°﹣36°=72°,同理得:∠ADE=36°,∵∠BAE=108°,AB=AE,∴∠ABE=36°,∴∠CBF=108°﹣36°=72°,∴BC=FC,∵BC=CD,∴CD=CF,∴∠CDF=∠CFD=(180°-72°)÷2=54°,∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
=108°,∴∠BAC=∠ACB=36°,∴∠ACD=108°﹣36°=72°,同理得:∠ADE=36°,∵∠BAE=108°,AB=AE,∴∠ABE=36°,∴∠CBF=108°﹣36°=72°,∴BC=FC,∵BC=CD,∴CD=CF,∴∠CDF=∠CFD=(180°-72°)÷2=54°,∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
所以①正确;
②∵∠ABE=∠ACB=36°,∠BAC=∠BAF,∴△ABF∽△ACB,∴![]() ,∴ABED=ACEG,∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,∴22=(2﹣FG)(4﹣FG),∴FG=3+
,∴ABED=ACEG,∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,∴22=(2﹣FG)(4﹣FG),∴FG=3+![]() >2(舍),FG=3﹣
>2(舍),FG=3﹣![]() ;
;
所以②正确;
③如图1,∵∠EBC=72°,∠BCD=108°,∴∠EBC+∠BCD=180°,∴EF∥CD,∵EF=CD=2,∴四边形CDEF是平行四边形,过D作DM⊥EG于M,∵DG=DE,∴EM=MG=![]() EG=
EG=![]() (EF﹣FG)=
(EF﹣FG)=![]() (2﹣3+
(2﹣3+![]() )=
)=![]() ,由勾股定理得:DM=
,由勾股定理得:DM=![]() =
=![]() =
=![]() ,∴(S四边形CDEF)2=EF2×DM2=4×
,∴(S四边形CDEF)2=EF2×DM2=4×![]() =10+2
=10+2![]() ;
;
所以③不正确;
④如图2,连接EC,∵EF=ED,∴CDEF是菱形,∴FD⊥EC,∵EC=BE=4﹣FG=4﹣(3﹣![]() )=1+
)=1+![]() ,∴S四边形CDEF=/span>
,∴S四边形CDEF=/span>![]() FDEC=2×
FDEC=2×![]() ,
,![]() ×FD×(1+
×FD×(1+![]() )=
)=![]() ,FD2=10﹣2
,FD2=10﹣2![]() ,∴DF2﹣DG2=10﹣2
,∴DF2﹣DG2=10﹣2![]() ﹣4=6﹣2
﹣4=6﹣2![]() ,所以④不正确;
,所以④不正确;
本题正确的有两个,故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的门票销售分两类:一类为散客门票,价格为
 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游 人,购买门票需要
人,购买门票需要 元
元(1)如果每人分别买票,求
 与
与 之间的函数关系式:
之间的函数关系式:(2)如果购买团体票,求
 与
与 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别住在A、B、C三个住宅区,A区有60人,B区有30人,C区有20人,三个区在同一条直线上,如图.该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )

A. A区 B. B区 C. C区 D. A、B两区之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】
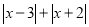 的最小值是______;
的最小值是______;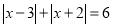 ,则x=_________
,则x=_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示,∠ABO=∠CBD=90°,若点A(2
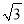 ,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )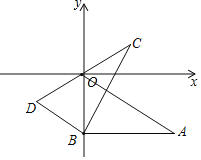
A. (2,2
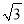 )B. (1,
)B. (1,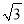 )C. (
)C. (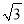 ,1)D. (2
,1)D. (2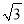 ,2)
,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
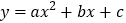 (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q(
 ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣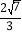 .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
相关试题

