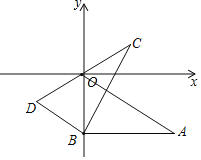
【题目】Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示,∠ABO=∠CBD=90°,若点A(2![]() ,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
A. (2,2![]() )B. (1,
)B. (1,![]() )C. (
)C. (![]() ,1)D. (2
,1)D. (2![]() ,2)
,2)
参考答案:
【答案】C
【解析】
过点C作CE垂直x轴于点E.先证明△ODB为等边三角形,求出OD、DB长,然后根据∠DCB=30°,求出CD的长,进而求出OC,最后求出OE,CE,即求出点C坐标.
.解:如图,过点C作CE垂直x轴于点E.
∵A(2![]() ,﹣2),
,﹣2),
∴OB=2,AB=2![]() ,
,
∵∠ABO=∠CBD=90°,
∴∠DBO=∠CBA=60°,
∵BO=BD,
∴∠D=DOB=60°,
DO=DB=BO=2,
∴∠BCD=30°,
CD=2BD=4,
∴CO=CD﹣OD=4﹣2=2,
∵∠COE=90°﹣∠COy=90°﹣60°=30°
∴CE=![]() OC=1,OE=
OC=1,OE=![]() ,
,
∴C(![]() ,1).
,1).
故选:C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017山东省莱芜市)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣
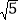 ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2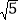 ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2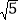 .其中正确结论的个数是( )
.其中正确结论的个数是( )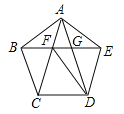
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】
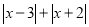 的最小值是______;
的最小值是______;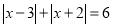 ,则x=_________
,则x=_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
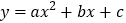 (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q(
 ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣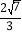 .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上) -
科目: 来源: 题型:
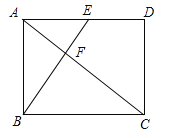
查看答案和解析>>【题目】(2017山东省莱芜市)如图,在矩形ABCD中,BE⊥AC分别交AC、AD于点F、E,若AD=1,AB=CF,则AE=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

相关试题

