【题目】某公司员工分别住在A、B、C三个住宅区,A区有60人,B区有30人,C区有20人,三个区在同一条直线上,如图.该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
![]()
A. A区 B. B区 C. C区 D. A、B两区之间
参考答案:
【答案】A
【解析】
此题考查了比较线段的长短
根据题意分别计算停靠点分别在各点是员工步行的路程和,选择最小的即可解.
∵当停靠点在A区时,所有员工步行到停靠点路程和是:15×100+10×300=4500m;
当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000m;
当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000m.
∴当停靠点在A区时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在A区.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,DC∥AB,AD=5,CD=3,sinA=sinB=
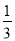 ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )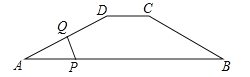
A.
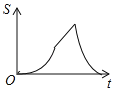 B.
B. 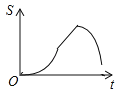
C.
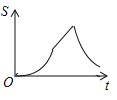 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在数轴上点A,B,C表示的数分别为﹣2,0,6.点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)AB= ,BC= ,AC= ;
(2)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.
①设运动时间为t,请用含有t的算式分别表示出AB,BC,AC;
②在①的条件下,请问:BC﹣AB的值是否随着运动时间t的变化而变化?若变化,请说明理由:若不变,请求其值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的门票销售分两类:一类为散客门票,价格为
 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游 人,购买门票需要
人,购买门票需要 元
元(1)如果每人分别买票,求
 与
与 之间的函数关系式:
之间的函数关系式:(2)如果购买团体票,求
 与
与 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017山东省莱芜市)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣
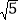 ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2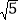 ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2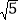 .其中正确结论的个数是( )
.其中正确结论的个数是( )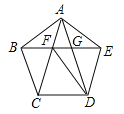
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】
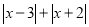 的最小值是______;
的最小值是______;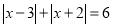 ,则x=_________
,则x=_________
相关试题

