【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
参考答案:
【答案】①③.
【解析】解:①∵a<0,∴抛物线开口向下,∵图象与x轴的交点A、B的横坐标分别为﹣3,1,∴当x=﹣4时,y<0,即16a﹣4b+c<0;
故①正确;
②∵图象与x轴的交点A、B的横坐标分别为﹣3,1,∴抛物线的对称轴是:x=﹣1,∵P(﹣5,y1),Q(![]() ,y2),﹣1﹣(﹣5)=4,
,y2),﹣1﹣(﹣5)=4,![]() ﹣(﹣1)=3.5,由对称性得:(﹣4.5,y3)与Q(
﹣(﹣1)=3.5,由对称性得:(﹣4.5,y3)与Q(![]() ,y2)是对称点,∴则y1<y2;
,y2)是对称点,∴则y1<y2;
故②不正确;
③∵![]() =﹣1,∴b=2a,当x=1时,y=0,即a+b+c=0,3a+c=0,a=﹣
=﹣1,∴b=2a,当x=1时,y=0,即a+b+c=0,3a+c=0,a=﹣![]() c;
c;
④要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的正半轴上,∴c=![]() ,与b=2a、a+b+c=0联立组成解方程组,解得b=﹣
,与b=2a、a+b+c=0联立组成解方程组,解得b=﹣![]() ;
;
同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的正半轴上,∴c=![]() ,与b=2a、a+b+c=0联立组成解方程组,解得b=﹣
,与b=2a、a+b+c=0联立组成解方程组,解得b=﹣![]() ;
;
同理当AC=BC时,在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无实数解.
经解方程组可知有两个b值满足条件.
故⑤错误.
综上所述,正确的结论是①③.
故答案为:①③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017山东省莱芜市)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣
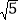 ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2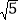 ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2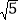 .其中正确结论的个数是( )
.其中正确结论的个数是( )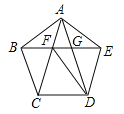
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】
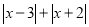 的最小值是______;
的最小值是______;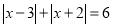 ,则x=_________
,则x=_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示,∠ABO=∠CBD=90°,若点A(2
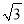 ,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )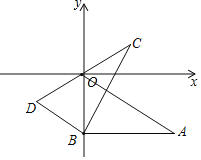
A. (2,2
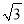 )B. (1,
)B. (1,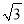 )C. (
)C. (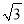 ,1)D. (2
,1)D. (2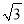 ,2)
,2) -
科目: 来源: 题型:
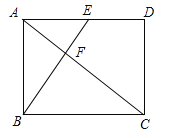
查看答案和解析>>【题目】(2017山东省莱芜市)如图,在矩形ABCD中,BE⊥AC分别交AC、AD于点F、E,若AD=1,AB=CF,则AE=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

-
科目: 来源: 题型:
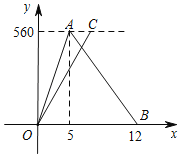
查看答案和解析>>【题目】一天,明明和强强相约到距他们村庄560米的博物馆游玩,他们同时从村庄出发去博物馆,明明到博物馆后因家中有事立即返回.如图是他们离村庄的距离y(米)与步行时间x(分钟)之间的函数图象,若他们出发后6分钟相遇,则相遇时强强的速度是_____米/分钟.
相关试题

