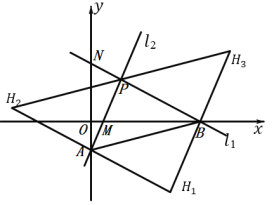
【题目】如图,直线 ![]() 1:y=kx+b 分别交 x 轴、y 轴于点 B(4,0)、N,直线
1:y=kx+b 分别交 x 轴、y 轴于点 B(4,0)、N,直线![]() 2:y=2x-1分别交 x 轴、y 轴于点 M、A,
2:y=2x-1分别交 x 轴、y 轴于点 M、A,![]() 1,
1,![]() 2 交点 P 的坐标(m,2),请根据图象所提供的信息解答下列问题:
2 交点 P 的坐标(m,2),请根据图象所提供的信息解答下列问题:

(1)当 x 时,kx+b≥2x-1;
(2)不等式 k![]() +b<0 的解集是 ;
+b<0 的解集是 ;
(3)在平面内是否存在一点 H,使得以A,B,P,H四点组成的四边形是平行四边形.若存在,直接写出点 H 的坐标,若不存在,说明理由.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ; (3)存在,点H的坐标为(
; (3)存在,点H的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求得点P的坐标,根据函数图象,即可求解;
(2)根据函数图象,即可求解;
(3)设点H的坐标为(a,n),分AB为对角线、AP为对角线及BP为对角线三种情况,利用平行四边形的性质(对角线互相平分)可求出点H的坐标.
(1)∵点P(m,2)在直线![]() 2:
2:![]() 上,
上,
令![]() ,则
,则![]() ,
,
∴点P的坐标为(![]() ,2),
,2),
观察函数图象,当![]() 时,直线
时,直线 ![]() 1在直线
1在直线![]() 2的上方,
2的上方,
∴当![]() 时,
时,![]() ;
;
(2)直线 ![]() 1:
1:![]() 分别交
分别交![]() 轴于点 B(4,0),
轴于点 B(4,0),
观察函数图象,当![]() 时,直线
时,直线 ![]() 1在
1在![]() 轴的下方,
轴的下方,
∴不等式![]() 的解集为:
的解集为:![]() ;
;
(3)存在,设点H的坐标为(a,n),
令![]() ,则
,则![]() ,
,
∴点A的坐标为(0,![]() ),
),
∵点B的坐标为(4,0),点P的坐标为(![]() ,2),
,2),
分三种情况考虑,如图所示:
①当AB为对角线时,
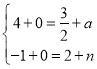
解得: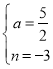 ,
,
∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() );
);
②当AP为对角线时,
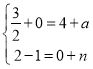 ,
,
解得: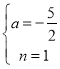 ,
,
∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() );
);
③当BP为对角线时,
 ,
,
解得: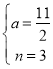 ,
,
∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() );
);
综上所述:在平面直角坐标系中存在点H,使以点A,B,P,H为顶点的四边形是平行四边形,点H的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .
-
科目: 来源: 题型:
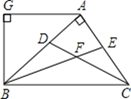
查看答案和解析>>【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
A.
 B.
B. 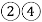 C.
C.  D.
D. 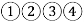
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过 1 千克的,按每千克 22 元收费;超过 1 千克,超过的部分按每千克 15元收费.乙公司表示:按每千克 16 元收费,另加包装费 3 元.设小明快递物品x 千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用 y(元)与 x(千克)之间的函数关系式;
(2)当
 为何值时小明选择乙快递公司更省钱?
为何值时小明选择乙快递公司更省钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在六边形
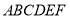 中,
中,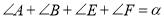 ,
,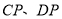 分别平分
分别平分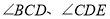 ,则
,则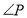 的度数为( )
的度数为( )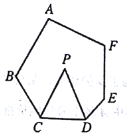
A.
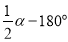 B.
B.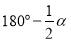 C.
C.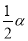 D.
D.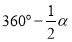
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,已知点A、B的坐标分别为A(a,0),B(b,0),a,b满足方程组
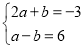 ,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.
,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.(1)求A、B、C三点的坐标;
(2)坐标系中是否存在点P(m,m),使S△PAB=
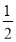 S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.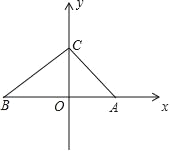
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
相关试题

