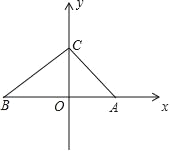
【题目】在直角坐标系中,已知点A、B的坐标分别为A(a,0),B(b,0),a,b满足方程组![]() ,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.
,C为y轴正半轴上一点,且△ABC的面积S△ABC=6.
(1)求A、B、C三点的坐标;
(2)坐标系中是否存在点P(m,m),使S△PAB=![]() S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(1,0),B(﹣5,0),C(0,2);(2)P点坐标为(1,1)或(﹣1,﹣1).
【解析】
(1)解方程得到A、B点的坐标,即可得到AB=6,根据三角形面积公式解得OC=2,即可得出C点的坐标;
(2)先计算出S△PAB=3,根据三角形面积公式解得|m|=1,从而确定P点坐标.
(1)解方程组![]() 得
得![]() ,
,
∴A(1,0),B(﹣5,0),
∴AB=6,
∵S△ABC=![]() ABOC,
ABOC,
∴6=![]() ,
,
解得OC=2,
∴C(0,2);
(2)存在,
∵S△ABC=6,S△PAB=![]() S△ABC,
S△ABC,
∴S△PAB=![]() AB|m|=3,
AB|m|=3,
∴|m|=1.
∴m=±1,
∴P点坐标为(1,1)或(﹣1,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过 1 千克的,按每千克 22 元收费;超过 1 千克,超过的部分按每千克 15元收费.乙公司表示:按每千克 16 元收费,另加包装费 3 元.设小明快递物品x 千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用 y(元)与 x(千克)之间的函数关系式;
(2)当
 为何值时小明选择乙快递公司更省钱?
为何值时小明选择乙快递公司更省钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 1:y=kx+b 分别交 x 轴、y 轴于点 B(4,0)、N,直线
1:y=kx+b 分别交 x 轴、y 轴于点 B(4,0)、N,直线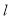 2:y=2x-1分别交 x 轴、y 轴于点 M、A,
2:y=2x-1分别交 x 轴、y 轴于点 M、A, 1,
1, 2 交点 P 的坐标(m,2),请根据图象所提供的信息解答下列问题:
2 交点 P 的坐标(m,2),请根据图象所提供的信息解答下列问题:
(1)当 x 时,kx+b≥2x-1;
(2)不等式 k
 +b<0 的解集是 ;
+b<0 的解集是 ;(3)在平面内是否存在一点 H,使得以A,B,P,H四点组成的四边形是平行四边形.若存在,直接写出点 H 的坐标,若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在六边形
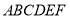 中,
中,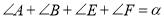 ,
,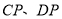 分别平分
分别平分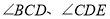 ,则
,则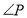 的度数为( )
的度数为( )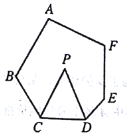
A.
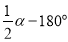 B.
B.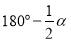 C.
C.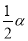 D.
D.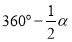
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在正方形 ABCD 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.
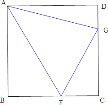
(2)如图,在 Rt△ABC 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,
①写出 BE,CF,EF 之间的数量关系,并证明.
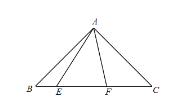
②若将(2)中的△AEF 绕点 A 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.
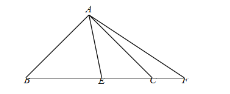
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则
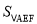 = .
= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.
 B.
B.  C.
C. 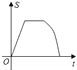 D.
D. 
相关试题

