【题目】在矩形ABCD中,AB=1,BC=2,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C'.
(1)如果C'落在线段AB的延长线上.
①在图①中补全图形;
②求线段BP的长度;
(2)如图②,设直线AP与CC'的交点为M,求证:BM⊥DM.

参考答案:
【答案】(1)①见解析;②PB=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)①根据要求画出图形即可;
②连接AC,作PH⊥AC于H.则△APB≌△APH,同侧AB=AH=1,PB=PH,设PB=PH=x,利用勾股定理构建方程即可;
(2)如图②中,连接AC、BD交于点O.连接OM.只要证明A、B、M、C、D五点共圆,即可解决问题;
解:(1)①如图①所示:
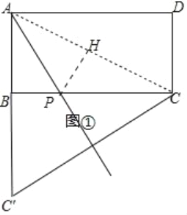
②连接AC,作PH⊥AC于H.则△APB≌△APH,
∴AB=AH=1,PB=PH,设PB=PH=x,
∵AC=![]() =
=![]() ,
,
∴CH=![]() ﹣1,
﹣1,
在Rt△PCH中,x2+(![]() ﹣1)2=(2﹣x)2,
﹣1)2=(2﹣x)2,
解得x=![]() ,
,
∴PB=![]() .
.
(2)如图②中,连接AC、BD交于点O.连接OM.
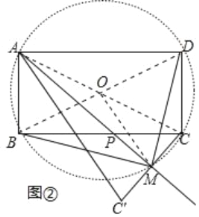
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∵∠AMC=90°,
∴OM=OA=OB=OC=OD,
∴A、B、M、C、D五点共圆,
∵BD是直径,
∴∠BMD=90°,
∴BM⊥DM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)如图,一次函数y=kx+b与反比例函数
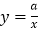 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥
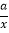 的解集;
的解集;(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
-
科目: 来源: 题型:
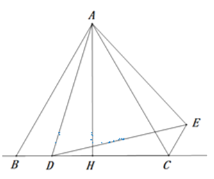
查看答案和解析>>【题目】如图,在
 中,
中,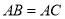 ,
,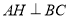 垂足为
垂足为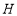 ,
,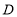 为直线
为直线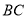 上一动点(不与点
上一动点(不与点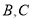 重合),在
重合),在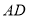 的右侧作
的右侧作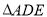 ,使得
,使得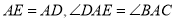 ,连接
,连接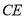 .
.(1)求证:
 ;
;(2)当
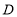 在线段
在线段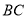 上时
上时① 求证:
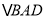 ≌
≌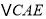 ;
; ② 若
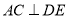 , 则
, 则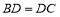 ;
;(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
相关试题

