【题目】(9分)如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
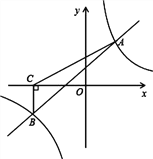
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b≥![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
参考答案:
【答案】(1)![]() ;y=x+1;(2)x>2或-3<x<0;(3)5.
;y=x+1;(2)x>2或-3<x<0;(3)5.
【解析】试题分析:(1)首先根据两函数的交点A(2,3),求出反比例函数中m的值,从而确定反比例函数的关系式;根据B(-3,n)在反比例函数图象上可求得n的值,将A、B两点的坐标分别代入一次函数y=kx+b中,可得关于k和b的二元一次方程组,解此方程组就可得到一次函数的关系式;
(2)kx+b≥![]() 为一次函数大于反比例函数的部分,根据函数图象和点A,B坐标即可求出kx+b≥
为一次函数大于反比例函数的部分,根据函数图象和点A,B坐标即可求出kx+b≥![]() 的解集。
的解集。
(3)以BC为底,点A和点B的横坐标之差为高,即可求出△ABC的面积。
解:(1)从图象可知A的坐标是(2,3),B的坐标是(﹣3,n),
把A的坐标代入反比例函数的解析式得:k=6,
即反比例函数的解析式是y=![]() ,
,
把B的坐标代入反比例函数的解析式得:n=-2,
即B的坐标是(-3,-2),
把A、B的坐标代入一次函数的解析式得:
![]() ,
,
解得:k=1,b=1.
即一次函数的解析式是y=x+1;
(2)∵由图象可知使一次函数的值大于反比例函数的值的x取值范围是x>2或![]() <x<0.
<x<0.
∴不等式kx+b≥![]() 的解集为x>2或-3<x<0.
的解集为x>2或-3<x<0.
(3)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划组织师生共435人参加一次大型公益活动,如果租用5辆小客车和6辆大客车恰好全部坐满,已知每辆大客车的乘客座位数比小客车多12个.
(1) 求每辆小客车和每辆大客车的乘客座位数;
(2) 由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场普通门票价格40元/张,为了促销,新推出两种办卡方式:
①白金卡售价200元/张,每次凭卡另收取20元;
②钻石卡售价1000元/张,每次凭卡不再收费.
促销期间普通门票正常出售,两种优惠卡不限次数,设去游乐场玩x次时,所需总费用为y元.
(1)分别写出选择白金卡、普通门票消费时,y与x之间的函数关系式.
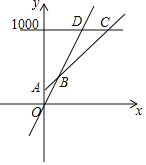
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B,C的坐标.
(3)请根据图象,直接写出选择哪种消费方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2.若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,下图①为点P,Q的“相关矩形”的示意图.

已知点A的坐标为(1,0),
(1)若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
(2)点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(3)若点D的坐标为(4,2),将直线y=2x+b平移,当它与点A,D的“相关矩形”没有公共点时,求出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=1,BC=2,点P是边BC上一点(点P不与点B,点C重合),点C关于直线AP的对称点为C'.
(1)如果C'落在线段AB的延长线上.
①在图①中补全图形;
②求线段BP的长度;
(2)如图②,设直线AP与CC'的交点为M,求证:BM⊥DM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
相关试题

