【题目】点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.

(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;
(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;
(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE之间有怎样的数量关系,直接写出结论不必证明.
参考答案:
【答案】(1)OE=OF.理由见解析;(2)补全图形如图所示见解析,OE=OF仍然成立;(3)CF=OE+AE或CF=OE﹣AE.
【解析】
(1)根据矩形的性质以及垂线,即可判定![]() ,得出OE=OF;
,得出OE=OF;
(2)先延长EO交CF于点G,通过判定![]() ,得出OG=OE,再根据
,得出OG=OE,再根据![]() 中,
中,![]() ,即可得到OE=OF;
,即可得到OE=OF;
(3)根据点P在射线OA上运动,需要分两种情况进行讨论:当点P在线段OA上时,当点P在线段OA延长线上时,分别根据全等三角形的性质以及线段的和差关系进行推导计算即可.
(1)OE=OF.理由如下:
如图1.
∵四边形ABCD是矩形,∴ OA=OC.
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵在![]() 和
和![]() 中,
中, ,∴
,∴![]() ,∴ OE=OF;
,∴ OE=OF;
(2)补全图形如图2,OE=OF仍然成立.证明如下:
延长EO交CF于点G.
∵![]() ,
,![]() ,∴ AE//CF,∴
,∴ AE//CF,∴![]() .
.
又∵点O为AC的中点,∴ AO=CO.
在![]() 和
和![]() 中,
中,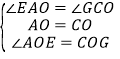 ,∴
,∴![]() ,∴ OG=OE,∴
,∴ OG=OE,∴![]() 中,
中,![]() ,∴ OE=OF;
,∴ OE=OF;
(3)CF=OE+AE或CF=OE-AE.
证明如下:①如图2,当点P在线段OA上时.
∵![]() ,
,![]() ,∴
,∴![]() ,由(2)可得:OF=OG,∴
,由(2)可得:OF=OG,∴![]() 是等边三角形,∴ FG=OF=OE,由(2)可得:
是等边三角形,∴ FG=OF=OE,由(2)可得:![]() ,∴ CG=AE.
,∴ CG=AE.
又∵ CF=GF+CG,∴ CF=OE+AE;
②如图3,当点P在线段OA延长线上时.
∵![]() ,
,![]() ,∴
,∴![]() ,同理可得:
,同理可得:![]() 是等边三角形,∴ FG=OF=OE,同理可得:
是等边三角形,∴ FG=OF=OE,同理可得:![]() ,∴ CG=AE.
,∴ CG=AE.
又∵ CF=GF-CG,∴ CF=OE-AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图左右并排的两颗大树的高度分别是AB=8米,CD=12米,两树的水平距离BD=5米,一观测者的眼睛高EF=1.6米,且E、B、D在一条直线上,当观测者的视线FAC恰好经过两棵树的顶端时,四边形ABDC的区域是观测者的盲区,则此时观测者与树AB的距离EB等于( )

A.8米 B.7米 C.6米 D.5米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形
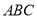 中,点
中,点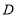 在线段
在线段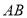 上,
上,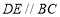 交
交 于点
于点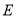 ,点
,点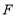 在直线
在直线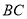 上,作直线
上,作直线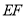 ,过点
,过点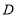 作直线
作直线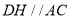 交直线
交直线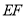 于点
于点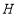 .
.
图1 图2 图3
(1)在如图1所示的情况下,求证:
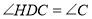 ;
;(2)若三角形
 不变,
不变, ,
, 两点的位置也不变,点
两点的位置也不变,点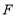 在直线
在直线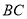 上运动.
上运动.①当点
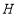 在三角形
在三角形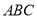 内部时,说明
内部时,说明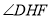 与
与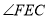 的数量关系:
的数量关系:②当点
 在三角形
在三角形 外部时,①中结论是否依然成立?若不成立,
外部时,①中结论是否依然成立?若不成立,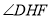 与
与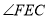 又有怎样的数量关系?请在图2中画图探究,并说明理由.
又有怎样的数量关系?请在图2中画图探究,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD相交于点O,∠ABC∶∠BAD=1∶2,AC∥BE,CE∥BD.
(1)求∠DBC的度数;
(2)求证:四边形OBEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
 在平面直角坐标系中按图中箭头所示方向运动,第
在平面直角坐标系中按图中箭头所示方向运动,第 次从原点运动到点
次从原点运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,
, 按这样的运动规律,经过第
按这样的运动规律,经过第 次运动后,动点
次运动后,动点 的坐标是( )
的坐标是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
级别
家庭的文化教育消费金额
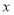 (元)
(元)户数
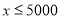
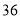

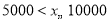
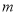
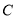
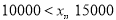
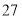
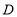
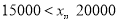
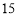
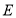
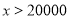
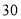
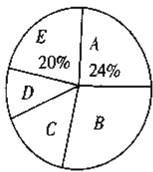
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有___________户,表中
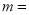 ___________;
___________;(2)在扇形统计图中,
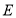 组所在扇形的圆心角为多少度?
组所在扇形的圆心角为多少度?(3)这个社区有
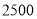 户家庭,请你估计年文化教育消费在
户家庭,请你估计年文化教育消费在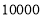 元以上的家庭有多少户.
元以上的家庭有多少户.
相关试题

