【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高,某社区为了了解家庭对于文化教育的消费情况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调查,根据调查结果绘制成如下两幅不完整的统计图表.
级别 | 家庭的文化教育消费金额 | 户数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
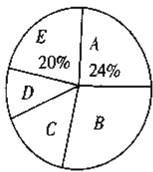
请你根据统计图表提供的信息,解答下列问题:
(1)本次被调查的家庭有___________户,表中![]() ___________;
___________;
(2)在扇形统计图中,![]() 组所在扇形的圆心角为多少度?
组所在扇形的圆心角为多少度?
(3)这个社区有![]() 户家庭,请你估计年文化教育消费在
户家庭,请你估计年文化教育消费在![]() 元以上的家庭有多少户.
元以上的家庭有多少户.
参考答案:
【答案】(1)答案为:![]() ,
,![]() ;(2)
;(2)![]() 组所在扇形的圆心角为
组所在扇形的圆心角为![]() ;(3)1200(户)
;(3)1200(户)
【解析】
(1)依据A组或E组数据,即可得到样本容量,进而得出m的值;
(2)利用圆心角计算公式,即可得到E组所在扇形的圆心角;
(3)依据家庭年文化教育消费10000元以上的家庭所占的比例,即可得到家庭年文化教育消费10000元以上的家庭的数量.
解:(1)本次被调查的家庭有:36÷24%=150,
m=150-36-27-15-30=42,
故答案为:150,42;
(2)![]() 组所在扇形的圆心角为
组所在扇形的圆心角为![]() ;
;
(3)年文化教育消费![]() 元以上的家庭有
元以上的家庭有![]() (户)
(户)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.

(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;
(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;
(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE之间有怎样的数量关系,直接写出结论不必证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD相交于点O,∠ABC∶∠BAD=1∶2,AC∥BE,CE∥BD.
(1)求∠DBC的度数;
(2)求证:四边形OBEC是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
 在平面直角坐标系中按图中箭头所示方向运动,第
在平面直角坐标系中按图中箭头所示方向运动,第 次从原点运动到点
次从原点运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,第
,第 次接着运动到点
次接着运动到点 ,
, 按这样的运动规律,经过第
按这样的运动规律,经过第 次运动后,动点
次运动后,动点 的坐标是( )
的坐标是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=-
 x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
x2+bx+c与x轴相交于点A,C,与y轴相交于点B,连接AB,BC,点A的坐标为(2,0),tan∠BAO=2,以线段BC为直径作⊙M交AB于点D,过点B作直线l∥AC,与抛物线和⊙M的另一个交点分别是E,F.
(1)求该抛物线的函数表达式;
(2)求点C的坐标和线段EF的长;
(3)如图2,连接CD并延长,交直线l于点N,点P,Q为射线NB上的两个动点(点P在点Q的右侧,且不与N重合),线段PQ与EF的长度相等,连接DP,CQ,四边形CDPQ的周长是否有最小值?若有,请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是________、________.
(2)将△ABC平移后使点C与点D重合,点A、B分别与点E、F重合,画出△DEF.并直接写出E点的坐标 ,F点的坐标 .
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为___ _____.
(4)求
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
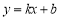 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数 的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6,
的图象交于C、D两点,DE⊥x轴于点E.已知C点的坐标是(6, ),DE=3.
),DE=3.(1)求反比例函数与一次函数的解析式.
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?

相关试题

