【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
试题解析:(1)连接OD,
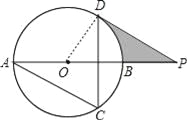
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB=![]() ×3×3
×3×3![]() ﹣
﹣![]() cm2
cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决问题
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小而解决问题的策略般要进行一定的转化,其中“求差法”就是常用的方法之一,所谓“求差法”:就是通过求差、变形,并利用差的符号来确定它们的大小,即要比较代数式
 的大小,只要求出它们的差
的大小,只要求出它们的差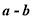 ,若
,若 ,则
,则 ;若
;若 ,则
,则 .若
.若 ,则
,则 ,
,请你用“求差法”解决以下问题
(1)若P=m2-2m-3,Q=m2-2m-1,比较
 的大小关系;
的大小关系;(2)制作某产品有两种用料方案方案一:用3块
 型钢板,用7块
型钢板,用7块 型钢板;方案二:用2块
型钢板;方案二:用2块 型钢板,用8块
型钢板,用8块 型钢板;
型钢板; 型钢板的面积比
型钢板的面积比 型钢板的面积大,设每块
型钢板的面积大,设每块 型钢板的面积为
型钢板的面积为 ,每块B型钢板的面积为
,每块B型钢板的面积为 ,从省料角度考虑,应选哪种方案?
,从省料角度考虑,应选哪种方案?(3)试比较图1和图2中两个矩形周长
 、
、 的大小.
的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,在平面直角坐标系中,
 是
是 轴正半轴上一点,
轴正半轴上一点, 是第四象限一点,
是第四象限一点, 轴,交
轴,交 轴负半轴于
轴负半轴于 ,且(a-2)+|b+3|=0,
,且(a-2)+|b+3|=0, 四边形AOBC=12.
四边形AOBC=12.(1)求
 点坐标
点坐标(2)如图二,设
 为线段
为线段 上一动点(点
上一动点(点 不与点
不与点 重合),求证:∠ADB+∠DBC-∠OAD=180°
重合),求证:∠ADB+∠DBC-∠OAD=180°(3)如图三,当
 点在线段
点在线段 上运动(点
上运动(点 不与点
不与点 重合),
重合), 点在线段
点在线段 上运动(点
上运动(点 不与点
不与点 重合)时,连接
重合)时,连接 、
、 作∠OAD、∠DEB的平分线交于
作∠OAD、∠DEB的平分线交于 点,请你探索∠AFE与∠ADE之间的关系,并说明理由.
点,请你探索∠AFE与∠ADE之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,
 )三点.
)三点.(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm.动点P、Q分别从点A、C以2cm/s的速度同时出发.动点P沿AB向终点B运动,动点Q沿CD向终点D运动,连结PQ交对角线AC于点O.设点P的运动时间为t(s).

(1)求OC的长.
(2)当四边形APQD是矩形时,直接写出t的值.
(3)当四边形APCQ是菱形时,求t的值.
(4)当△APO是等腰三角形时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )

A.7:20 B.7:30 C.7:45 D.7:50
相关试题

