【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2. 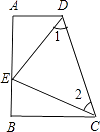
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
参考答案:
【答案】
(1)证明:∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中, ![]() ,
,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC
(2)解:∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形
【解析】(1)易证DE=CE,即可证明RT△ADE≌RT△BEC,可得AD=BE,即可解题;(2)由RT△ADE≌RT△BEC可得∠AED=∠BCE,即可求得∠DEC=90°,即可解题.
【考点精析】关于本题考查的等腰直角三角形,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=﹣2×32 , b=(﹣2×3)2 , c=﹣(2×3)2 , 则下列大小关系中正确的是( )
A.a>b>c
B.b>c>a
C.b>a>c
D.c>a>b -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)﹣(﹣5)﹣6+(﹣4)
(2)(﹣7)×(﹣5)+30÷(﹣15)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.连接MB和MC,当△OCE∽△OBC时,判断四边形AEMC的形状,并给出证明;
(3)有一动点P在(1)中的抛物线上运动,是否存在点P,以点P为圆心作圆能和直线AC和x轴同时相切 ,若存在,求出圆心P的坐标;若不存在,请说明理由.
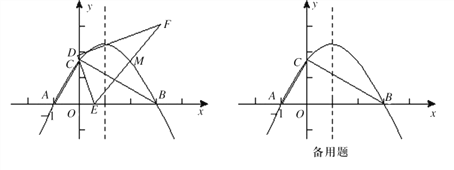
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.
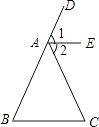
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
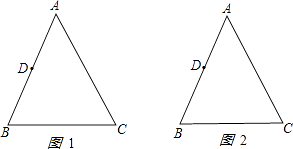
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2等于( )
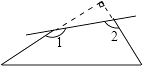
A.270°
B.180°
C.135°
D.90°
相关试题

