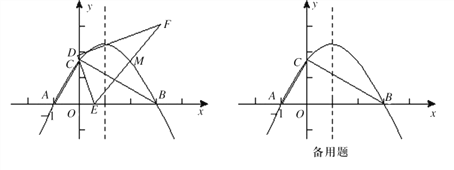
【题目】在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0).
(1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF所在直线与(1)中的抛物线交于第一象限的点M.连接MB和MC,当△OCE∽△OBC时,判断四边形AEMC的形状,并给出证明;
(3)有一动点P在(1)中的抛物线上运动,是否存在点P,以点P为圆心作圆能和直线AC和x轴同时相切 ,若存在,求出圆心P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)B(3,0),C(0, ![]() )过A、B、C三点的抛物线解析式为
)过A、B、C三点的抛物线解析式为![]() ;
;
(2)四边形AEMC是菱形,证明见解析;
(3)存在点P满足条件,点P坐标为(2, ![]() )或(6,-7
)或(6,-7![]() )
)
【解析】(1)解:(1)B(3,0),C(0, ![]() ).
).
∵A(—1,0)B(3,0),∴可设过A、B、C三点的抛物线为![]() .
.
又∵C(0, ![]() )在抛物线上,∴,解得.
)在抛物线上,∴,解得.
∴经过A、B、C三点的抛物线解析式为![]() .
.
(2)四边形AEMC是菱形.
当△OCE∽△OBC时,则错误!未找到引用源。.
∵OC=错误!未找到引用源。,∴![]()
错误!未找到引用源。∴OE=1.
∴E(1,0)在抛物线对称轴上,∴△CAE为等边三角形,∴∠AEC=∠A=60°.
又∵∠CEM=60°, ∴∠MEB=∠AEC=60°.
∴点C与点M关于抛物线的对称轴对称.
C(0,错误!未找到引用源。),∴M(2,错误!未找到引用源。).
∴MC=AE=2, MC∥AE
∴四边形AEMC是平行四边形。
∵AC=CM=2
∴四边形AEMC是菱形.
(3)由⊙P与直线AC和x轴同时相切易知点P在两线夹角的平分线上,
①当在x轴上方时,∠PAO=30°,设点P坐标为(x, ![]() ),过P作PQ⊥x轴,交点为Q,则AQ=
),过P作PQ⊥x轴,交点为Q,则AQ=![]() PQ,得x+1=
PQ,得x+1= ![]() (
(![]() )
)
解得,x1=2 ,x2=-1(舍去),所以点P坐标为(2, ![]() )
)
②当在x轴下方时,∠PAO=60°,设点P坐标为(x, ![]() ),过P作PQ⊥x轴,交点为Q,则
),过P作PQ⊥x轴,交点为Q,则![]() AQ=PQ,得
AQ=PQ,得![]() (x+1)= -(
(x+1)= -(![]() )
)
解得,x1=6 ,x2=-1(舍去),所以点P坐标为(6,-7![]() )
)
综上所述,存在点P满足条件,点P坐标为(2, ![]() )或(6,-7
)或(6,-7![]() )
)
-
科目: 来源: 题型:
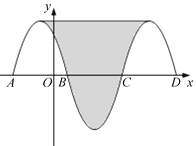
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=﹣2×32 , b=(﹣2×3)2 , c=﹣(2×3)2 , 则下列大小关系中正确的是( )
A.a>b>c
B.b>c>a
C.b>a>c
D.c>a>b -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)﹣(﹣5)﹣6+(﹣4)
(2)(﹣7)×(﹣5)+30÷(﹣15)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
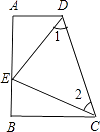
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE∥BC,AE平分∠DAC.求证:AB=AC.
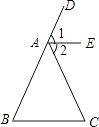
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
相关试题

