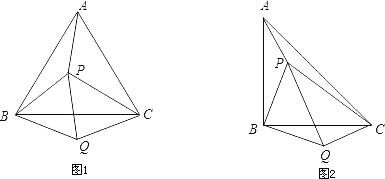
【题目】(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
参考答案:
【答案】(1)证明见解析(2)满足:![]()
【解析】
由旋转得△BAP≌△BCQ 满足:![]()
∴PA=CQ PB=BQ 由旋转得△BAP≌△BCQ
∵∠PBQ=60![]() ∴PA=CQ PB=BQ
∴PA=CQ PB=BQ
∴△PBQ为等边三角形 ∠PBQ=![]()
∴PB=PQ ∴![]()
∵PA![]() +PB
+PB![]() =PC
=PC![]() ∵
∵![]()
∴![]() ∴
∴![]()
∴∠PQC=90![]() ∴
∴![]()
(1)由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;
(2)由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
-
科目: 来源: 题型:
查看答案和解析>>【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宜传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,将获得的数据整理绘制成如下两幅不完整的统计图.(注:A为可回收物,B为厨余垃圾,C为有害垃圾,D为其它垃圾)
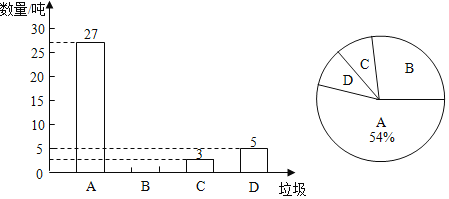
根据统计图提供的信息,解答下列问题:
(1)在这次抽样调查中,一共有 吨的生活垃圾;
(2)请将条形统计图补充完整;
(3)扇形统计图中,B所对应的百分比是 ,D所对应的圆心角度数是 ;
(4)假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,请估计每月产生的有害垃圾多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…,
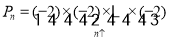 .
.(1)计算P7÷P8的值;
(2)计算2P2019+P2020的值;
(3)猜想2Pn与Pn+1的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-12)-(20)+(-8)-15.
(2)-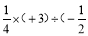 )3;
)3;
(3)-30×(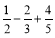 );
);
(4)(-6)2×(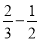 )-22;
)-22;(5)19
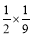 +(-1.5)÷(-3)2.
+(-1.5)÷(-3)2.
(6)2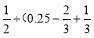 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:
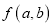 是关于
是关于 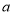 ,
,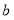 的多项式,如果
的多项式,如果 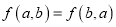 ,那么
,那么 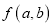 叫做“对称多项式”.例如,如果
叫做“对称多项式”.例如,如果 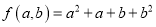 ,则
,则 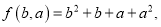 显然 ,所以
显然 ,所以 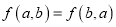 是“对称多项式”.
是“对称多项式”.(1)
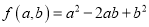 是“对称多项式”,试说明理由;
是“对称多项式”,试说明理由;(2)请写一个“对称多项式”,
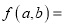 (不多于四项);
(不多于四项);(3)如果
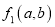 和
和 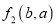 均为“对称多项式”,那么
均为“对称多项式”,那么 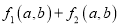 一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
相关试题

